
【题目】已知函数![]() ,其中
,其中![]() =2.71828…为自然数的底数.
=2.71828…为自然数的底数.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,求证:对任意的
时,求证:对任意的![]() ,
, ![]() .
.
【答案】(1)f(x)在R上单调递减.(2)证明见解析.
【解析】试题分析:(1)求函数的导数,利用函数单调性和导数之间的关系进行讨论即可;(2)对任意的x∈[0,+∞),![]() 转化为证明对任意的x∈[0,+∞),
转化为证明对任意的x∈[0,+∞),![]() ,即可,构造函数,求函数的导数,利用导数进行研究即可.
,即可,构造函数,求函数的导数,利用导数进行研究即可.
试题解析:(1)当a=0时,f(x)=ex(sinx﹣e),
则f′(x)=ex(sinx﹣e)+excosx=ex(sinx﹣e+cosx),
∵sinx+cosx= ![]() 、
、
∴sinx+cosx﹣e<0
故f′(x)<0
则f(x)在R上单调递减.
(2)当x≥0时,y=ex≥1,
要证明对任意的x∈[0,+∞),f(x)<0.
则只需要证明对任意的x∈[0,+∞),![]()
设g(a)=sinx﹣ax2+2a﹣e=(﹣x2+2)a+sinx﹣e,
看作以a为变量的一次函数,
要使sinx﹣ax2+2a﹣e<0,
则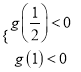 ,即
,即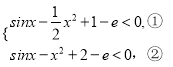 ,
,
∵sinx+1﹣e<0恒成立,∴①恒成立,
对于②,令h(x)=sinx﹣x2+2﹣e,
则h′(x)=cosx﹣2x,
设x=t时,h′(x)=0,即cost﹣2t=0.
∴t=![]() ,sint<
,sint<![]()
∴h(x)在(0,t)上,h′(x)>0,h(x)单调递增,在(t,+∞)上,h′(x)<0,h(x)单调递减,
则当x=t时,函数h(x)取得最大值h(t)=sint﹣t2+2﹣e=sint﹣(![]() )2+2﹣e
)2+2﹣e
=sint﹣![]() +2﹣e=
+2﹣e=![]() sin2t+sint+
sin2t+sint+![]() ﹣e=(
﹣e=(![]() +1)2+
+1)2+![]() ﹣e≤(
﹣e≤(![]() )2+
)2+![]() ﹣e=
﹣e=![]() ﹣e<0,
﹣e<0,
故④式成立,
综上对任意的x∈[0,+∞),f(x)<0.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知函数![]() ,
,![]() (
( ![]() 为常数).
为常数).
(1)求函数![]() 在点 (
在点 (![]() ,
,![]() )处的切线方程;
)处的切线方程;
(2)当![]() 时,设
时,设![]() ,若函数
,若函数![]() 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(sinx+cosx)2-2cos2x,
(1)求函数f(x)的最小正周期和单调递减区间;
(2)当x∈![]() 时,求f(x)的最大值和最小值
时,求f(x)的最大值和最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块半圆形空地,开发商计划建一个矩形游泳池ABCD及其矩形附属设施EFGH,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为O,半径为R,矩形的一边AB在直径上,点C、D、G、H在圆周上,E、F在边CD上,且![]() ,设
,设![]()
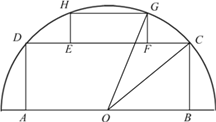
(1)记游泳池及其附属设施的占地面积为![]() ,求
,求![]() 的表达式;
的表达式;
(2)当![]() 为何值时,能符合园林局的要求?
为何值时,能符合园林局的要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)令![]() ,其图象上存在一点
,其图象上存在一点![]() ,使此处切线的斜率
,使此处切线的斜率![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)当![]() ,
, ![]() 时,方程
时,方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com