
【题目】如图,在圆柱![]() 中,点
中,点![]() 、
、![]() 分别为上、下底面的圆心,平面
分别为上、下底面的圆心,平面![]() 是轴截面,点
是轴截面,点![]() 在上底面圆周上(异于
在上底面圆周上(异于![]() 、
、![]() ),点
),点![]() 为下底面圆弧
为下底面圆弧![]() 的中点,点
的中点,点![]() 与点
与点![]() 在平面
在平面![]() 的同侧,圆柱
的同侧,圆柱![]() 的底面半径为1,高为2.
的底面半径为1,高为2.
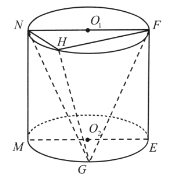
(1)若平面![]() 平面
平面![]() ,证明:
,证明:![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成线面角
所成线面角![]() 的正弦值等于
的正弦值等于![]() ,证明:平面
,证明:平面![]() 与平面
与平面![]() 所成锐二面角的平面角大于
所成锐二面角的平面角大于![]() .
.
【答案】(1)见证明;(2)见证明
【解析】
(1)由平面FNH⊥平面NHG,得FH⊥平面NHG,又由NG平面NHG,得证.(2)以O2为坐标原点,分别以O2G,O2E,O2O1为x、y、z轴建立空间坐标系O2﹣xyz,根据直线NH与平面NFG所成线面角α的正弦值等于![]() ,得到H点坐标,再将证明平面NHG与平面MNFE所成锐二面角的平面角大于
,得到H点坐标,再将证明平面NHG与平面MNFE所成锐二面角的平面角大于![]() .转化成证明平面NHG与平面MNFE所成锐二面角的余弦值小于
.转化成证明平面NHG与平面MNFE所成锐二面角的余弦值小于![]() 来解决.
来解决.
(1)由题知:面![]() 面
面![]() ,面
,面![]() 面
面![]() ,
,
因为![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() .
.
(2)以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
因为 ,所以
,所以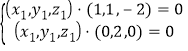 ,
,
所以![]() ,即法向量
,即法向量![]() .
.
因此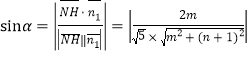
![]()
![]() .
.
所以![]() ,解得
,解得![]() ,
,![]() ,所以点
,所以点![]() .
.
设面![]() 的法向量
的法向量![]() ,
,
因为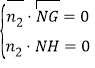 ,所以
,所以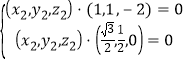 ,
,
所以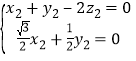 ,即法向量
,即法向量![]() .
.
因为面![]() 的法向量
的法向量![]() ,所以
,所以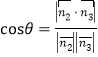
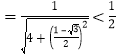 ,
,
所以面![]() 与面
与面![]() 所成锐二面角的平面角大于
所成锐二面角的平面角大于![]() .
.



 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,H为PC的中点,M为AH中点,PA=AC=2,BC=1.
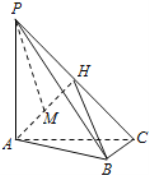
(Ⅰ)求证:AH⊥平面PBC;
(Ⅱ)求PM与平面AHB成角的正弦值;
(Ⅲ)在线段PB上是否存在点N,使得MN∥平面ABC,若存在,请说明点N的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为选拔A,B两名选手参加某项比赛,在选拔测试期间,他们参加选拔的5次测试成绩(满分100分)记录如下:
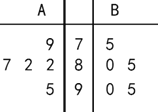
(1)从A,B两人的成绩中各随机抽取一个,求B的成绩比A低的概率;
(2)从统计学的角度考虑,你认为选派哪位选手参加比赛更合适?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为调查高二年级学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高(单位:![]() )在
)在![]() 内的男生人数有16人.
内的男生人数有16人.
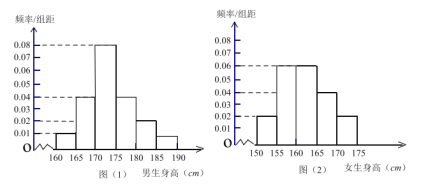
(Ⅰ)求在抽取的学生中,男女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的![]() 列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
|
| 总计 | |
男生人数 | |||
女生人数 | |||
总计 |
附:参考公式和临界值表:
 ,
,
| 5.024 | 6.635 | 7.879 | 10.828 |
| 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1到9的九个数字中取三个偶数四个奇数,试问:
(1)能组成多少个没有重复数字的七位数?
(2)上述七位数中三个偶数排在一起的有几个?
(3)在(1)中的七位数中,偶数排在一起、奇数也排在一起的有几个?
(4)在(1)中任意两偶数都不相邻的七位数有几个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区为了解居民参加体育锻炼情况,随机抽取18名男性居民,12名女性居民对他们参加体育锻炼的情况进行问卷调查.现按参加体育锻炼的情况将居民分成3类:甲类(不参加体育锻炼),乙类(参加体育锻炼,但平均每周参加体育锻炼的时间不超过5个小时),丙类(参加体育锻炼,且平均每周参加体育锻炼的时间超过5个小时),调查结果如下表:
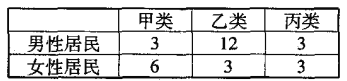
(1)根据表中的统计数据,完成下面列联表,并判断是否有![]() 的把握认为参加体育锻炼与否与性别有关?
的把握认为参加体育锻炼与否与性别有关?
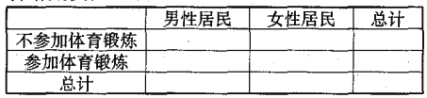
(2)从抽出的女性居民中再随机抽取2人进一步了解情况,求所抽取的2人中乙类,丙类各有1人的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com