
【题目】假设关于某设备的使用年限![]() (年)和所支出的维修费用
(年)和所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
若由资料知, ![]() 对
对![]() 呈线性相关关系,试求:
呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
参考公式:回归直线方程: ![]() .其中
.其中
(注: ![]() )
)
【答案】(1)![]() ;(2)12.38
;(2)12.38
【解析】试题分析: ![]() 先把数据列表,由题中所给的数据求出
先把数据列表,由题中所给的数据求出![]() ,
, ![]() ,根据最小二乘法做出线性回归方程的系数
,根据最小二乘法做出线性回归方程的系数![]() ,再根据样本中心点一定在线性回归方程上,求出
,再根据样本中心点一定在线性回归方程上,求出![]() 的值,从而得到线性回归方程;
的值,从而得到线性回归方程; ![]() 由
由![]() 取
取![]() ,计算出对应的
,计算出对应的![]() 的值,即使估计使用年限为
的值,即使估计使用年限为![]() 年时,维修费的估计值
年时,维修费的估计值
解析:(1)先把数据列表如下.
i | 1 | 2 | 3 | 4 | 5 | ∑ |
xi | 2 | 3 | 4 | 5 | 6 | 20 |
yi | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 | 25 |
xiyi | 4.4 | 11.4 | 22.0 | 32.5 | 42.0 | 112.3 |
x | 4 | 9 | 16 | 25 | 36 | 90 |
由表知,![]() =4,
=4,![]() =5,由公式可得:
=5,由公式可得:
![]() =
=![]() =
=![]() =1.23,
=1.23,![]() =
=![]() -
-![]()
![]() =5-1.23×4=0.08,
=5-1.23×4=0.08,
∴回归方程为![]() =1.23x+0.08.
=1.23x+0.08.
(2)由回归方程![]() =1.23x+0.08知,当x=10时,
=1.23x+0.08知,当x=10时,
![]() =1.23×10+0.08=12.38(万元).
=1.23×10+0.08=12.38(万元).
故估计使用年限为10年时维修费用是12.38万元.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】某学校为调查高二学生上学路程所需要的时间(单位:分钟),从高二年级学生中随机抽取![]() 名按上学所需要时间分组:第
名按上学所需要时间分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
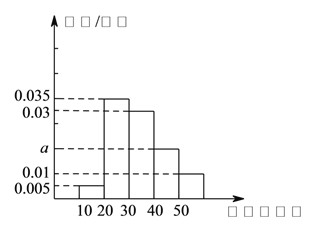
(![]() )根据图中数据求
)根据图中数据求![]() 的值.
的值.
(![]() )若从第
)若从第![]() ,
, ![]() ,
, ![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名新生参与交通安全问卷调查,应从第
名新生参与交通安全问卷调查,应从第![]() ,
, ![]() ,
, ![]() 组各抽取多少名新生?
组各抽取多少名新生?
(![]() )在(
)在(![]() )的条件下,该校决定从这
)的条件下,该校决定从这![]() 名学生中随机抽取
名学生中随机抽取![]() 名新生参加交通安全宣传活动,求第
名新生参加交通安全宣传活动,求第![]() 组至少有一志愿者被抽中的概率.
组至少有一志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据某气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示.过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即时间t(h)内沙尘暴所经过的路程s(km).

(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x2﹣2ax+b|(x∈R),给出下列命题:
①a∈R,使f(x)为偶函数;
②若f(0)=f(2),则f(x)的图象关于x=1对称;
③若a2﹣b≤0,则f(x)在区间[a,+∞)上是增函数;
④若a2﹣b﹣2>0,则函数h(x)=f(x)﹣2有2个零点.
其中正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个顶点为
的一个顶点为![]() ,半焦距为
,半焦距为![]() ,离心率
,离心率![]() ,又直线
,又直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点,且
两点,且![]() 为
为![]() 中点.
中点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求弦
,求弦![]() 的长;
的长;
(3)若点![]() 恰好平分弦
恰好平分弦![]() ,求实数
,求实数![]() ;
;
(4)若满足![]() ,求实数
,求实数![]() 的取值范围并求
的取值范围并求![]() 的值;
的值;
(5)设圆![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() 与点
与点![]() ,求
,求![]() 的最小值,并求此时圆
的最小值,并求此时圆![]() 的方程;
的方程;
(6)若直线![]() 是圆
是圆![]() 的切线,证明
的切线,证明![]() 的大小为定值.
的大小为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣mx+m,m∈R.
(1)求函数f(x)的单调区间.
(2)若f(x)≤0在x∈(0,+∞)上恒成立,求实数m的取值范围.
(3)在(2)的条件下,任意的0<a<b, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,已知直线l:x+y+a=0与点A(0,2),若直线l上存在点M满足|MA|2+|MO|2=10(O为坐标原点),则实数a的取值范围是( )
A.(﹣ ![]() ﹣1,
﹣1, ![]() ﹣1)
﹣1)
B.[﹣ ![]() ﹣1,
﹣1, ![]() ﹣1]
﹣1]
C.(﹣2 ![]() ﹣1,2
﹣1,2 ![]() ﹣1)
﹣1)
D.[﹣2 ![]() ﹣1,2
﹣1,2 ![]() ﹣1]
﹣1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若集合A={x|x2<2x},集合B={x|x< ![]() },则A∩(RB)等于( )
},则A∩(RB)等于( )
A.(﹣2, ![]() ]
]
B.(2,+∞)
C.(﹣∞, ![]() ]
]
D.D[ ![]() ,2)
,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com