
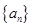 是等差数列,数列
是等差数列,数列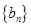 是等比数列,且对任意的
是等比数列,且对任意的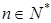 ,都有
,都有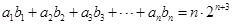 .
.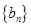 的首项为4,公比为2,求数列
的首项为4,公比为2,求数列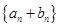 的前
的前 项和
项和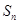 ;
;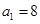 .
.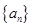 与
与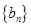 的通项公式;
的通项公式;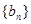 中是否存在某一项,它可以表示为该数列中其它
中是否存在某一项,它可以表示为该数列中其它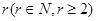 项的和?若存在,请求出该项;若不存在,请说明理由.
项的和?若存在,请求出该项;若不存在,请说明理由. (2) ①
(2) ① ②这样的项不存在
②这样的项不存在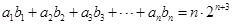 ,所以当
,所以当 时,
时, 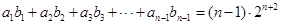 ,两式相减,得
,两式相减,得 ,
, 时,
时,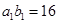 ,适合上式,从而
,适合上式,从而 ………………………3分
………………………3分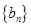 是首项为4,公比为2的等比数列,即
是首项为4,公比为2的等比数列,即 ,所以
,所以 ………………4分
………………4分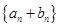 的前
的前 项和
项和 …………6分
…………6分 ,则
,则
 ,所以
,所以 ,
,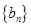 的公比为
的公比为 ,则
,则 对任意的
对任意的 恒成立 ………8分
恒成立 ………8分 对任意的
对任意的 恒成立,
恒成立,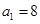 ,故
,故 ,且
,且 …………………………………10分
…………………………………10分 ……………………………………………11分
……………………………………………11分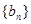 中第k项可以表示为该数列中其它
中第k项可以表示为该数列中其它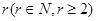 项
项
 ,从而
,从而 ,易知
,易知 (*)……………13分
(*)……………13分 ,
, ,此与(*)矛盾,从而这样的项不存在……………………………16分
,此与(*)矛盾,从而这样的项不存在……………………………16分 求通项,等比数列求和
求通项,等比数列求和 求
求 是常考的知识点,
是常考的知识点,


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源:不详 题型:单选题
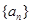 中,如果存在常数
中,如果存在常数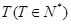 ,使得
,使得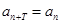 对于任意正整数
对于任意正整数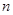 均成立,那么 就称数列
均成立,那么 就称数列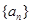 为周期数列,其中
为周期数列,其中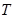 叫做数列
叫做数列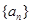 的周期. 已知数列
的周期. 已知数列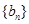 满足
满足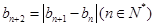 ,若
,若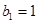 ,
,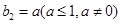 ,当数列
,当数列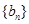 的周期为
的周期为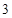 时,则数列
时,则数列 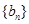 的前
的前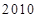 项的和
项的和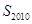 等于( )
等于( )A.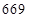 | B.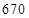 | C.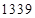 | D.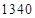 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
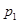 ,恰好
,恰好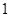 次正面向上的概率为
次正面向上的概率为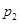 ;等比数列
;等比数列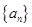 满足:
满足: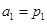 ,
,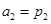
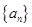 的通项公式;
的通项公式;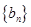 满足:
满足: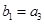 ,
,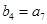 ,求等差数列
,求等差数列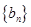 的前
的前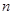 项和
项和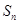 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com