
| A、a1=10 |
| B、a2=13 |
| C、a3=12 |
| D、以上均不正确 |
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| A、4 | ||
B、
| ||
| C、2 | ||
D、2
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 2014年巴西世界杯刚结束,某足球协会为了调查球迷对本届世界杯的了解情况,组织了“世界杯你问我答一百问”活动,该协会从参加活动的球迷(人数不少于1000人)中随机抽取12名球迷.进行世界杯知识问卷测试,测试成绩(百分制)以茎叶图形式表示如右图所示,根据主办方标准.测试成绩低于80分的为“伪球迷”,不低于80分的为“真球迷”.
2014年巴西世界杯刚结束,某足球协会为了调查球迷对本届世界杯的了解情况,组织了“世界杯你问我答一百问”活动,该协会从参加活动的球迷(人数不少于1000人)中随机抽取12名球迷.进行世界杯知识问卷测试,测试成绩(百分制)以茎叶图形式表示如右图所示,根据主办方标准.测试成绩低于80分的为“伪球迷”,不低于80分的为“真球迷”.查看答案和解析>>
科目:高中数学 来源: 题型:
| cosA |
| cosB |
| 2c-a |
| b |
| 3 |
3
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
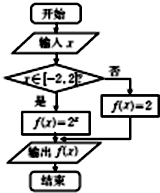 阅读如图所示的程序框图,如果输出的函数值在区间[
阅读如图所示的程序框图,如果输出的函数值在区间[| 1 |
| 4 |
| 1 |
| 2 |
| A、[-2,-1] |
| B、(-∞,-1] |
| C、[-1,2] |
| D、[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、“p∨q”为真 |
| B、“p∧q”为真 |
| C、p真q假 |
| D、p,q均为假 |
查看答案和解析>>
科目:高中数学 来源: 题型:
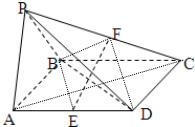 已知四棱锥P-ABCD是底面为平行四边形,面PAB⊥面ABCD,△PAB为正三角形,且AB=
已知四棱锥P-ABCD是底面为平行四边形,面PAB⊥面ABCD,△PAB为正三角形,且AB=| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com