
【题目】已知函数![]() ,其中
,其中![]() 且
且![]() ,若
,若![]() ,
, ![]() 在
在![]() 处切线的斜率为
处切线的斜率为![]() .
.
(1)求函数![]() 的解析式及其单调区间;
的解析式及其单调区间;
(2)若实数![]() 满足
满足![]() ,且
,且![]() 对于任意
对于任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由导数几何意义![]() ,结合
,结合![]() ,列方程组并解得
,列方程组并解得![]() ,
, ![]() ,根据导函数符号变化规律可得函数单调区间,(2)结合函数极值点分类讨论
,根据导函数符号变化规律可得函数单调区间,(2)结合函数极值点分类讨论![]() ,确定
,确定![]() 所在单调区间,再根据函数单调性验证是否满足题意,从而求出实数
所在单调区间,再根据函数单调性验证是否满足题意,从而求出实数![]() 的取值范围.
的取值范围.
试题解析:(1)由于![]() 且
且![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,即
,即![]() ,
,
故![]() ,即
,即![]() ,
, ![]() ,
,
因此![]() .
.
令![]() ,则
,则![]() ,即
,即![]() 在
在![]() 上单调递增,
上单调递增,
由于![]() ,则
,则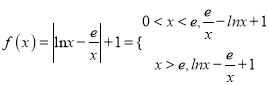 ,
,
故当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递增.
单调递增.
因此![]() 的单调递减区间为
的单调递减区间为![]() ,
, ![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)当![]() 时,取
时,取![]() ,则
,则![]() ,
,
由于![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,不合题意,故舍去;
,不合题意,故舍去;
当![]() 时,由抽屉原理可知
时,由抽屉原理可知![]() ,则
,则![]() ,
,
若![]() ,由于
,由于![]() 在
在![]() 上单调递减,则
上单调递减,则![]() 成立;
成立;
若![]() ,
, ![]() ,则
,则![]() ,
,
故![]() ,
,
由于![]() ,则
,则![]() ,
, ![]() (当且仅当
(当且仅当![]() 时取“=”)
时取“=”)
故![]() (当且仅当
(当且仅当![]() 时取“=”)
时取“=”)
由于![]() ,故上式无法取“=”,
,故上式无法取“=”,
因此![]() 恒成立,
恒成立, ![]() .
.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:
【题目】“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的![]() 城市和交通拥堵严重的
城市和交通拥堵严重的![]() 城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:
城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:
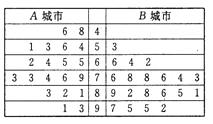
(Ⅰ)根据茎叶图,比较两城市满意度评分的平均值的大小及方差的大小(不要求具体解答过程,给出结论即可);
(Ⅱ)若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认同”,请根据此样本完成此列联表,并局此样本分析是否有95%的把握认为城市拥堵与认可共享单车有关;
(Ⅲ)若此样本中的![]() 城市和
城市和![]() 城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自
城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自![]() 城市的概率是多少?
城市的概率是多少?
|
| 合计 | |
认可 | |||
不认可 | |||
合计 |
附: 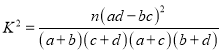
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在测试中,客观题难度的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度, ![]() 为答对该题的人数,
为答对该题的人数, ![]() 为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
题号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如下表所示(“√”表示答对,“×”表示答错):
| 1 | 2 | 3 | 4 | 5 |
1 | × | √ | √ | √ | √ |
2 | √ | √ | √ | √ | × |
3 | √ | √ | √ | √ | × |
4 | √ | √ | √ | × | × |
5 | √ | √ | √ | √ | √ |
6 | √ | × | × | √ | × |
7 | × | √ | √ | √ | × |
8 | √ | × | × | × | × |
9 | √ | √ | × | × | × |
10 | √ | √ | √ | √ | × |
(Ⅰ)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表,并估计这120名学生中第5题的实测答对人数;
题号 | 1 | 2 | 3 | 4 | 5 |
实测答对人数 | |||||
实测难度 |
(Ⅱ)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率;
(Ⅲ)定义统计量![]() ,其中
,其中![]() 为第
为第![]() 题的实测难度,
题的实测难度, ![]() 为第
为第![]() 题的预估难度
题的预估难度![]() .规定:若
.规定:若![]() ,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了![]() 名观众进行调查,其中女性有
名观众进行调查,其中女性有![]() 名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
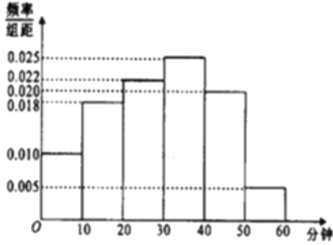
将日均收看该体育节目时间不低于![]() 分钟的观众称“体育述”,已知“体育迷”中
分钟的观众称“体育述”,已知“体育迷”中![]() 名女性.
名女性.
(1)根据已知条件完成下面的![]() 列联表,并据此资料你是否认为“体育迷”与性別有关?
列联表,并据此资料你是否认为“体育迷”与性別有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
(2)将日均收看该体育项目不低于![]() 分钟的观众称为“超级体育迷”,已知“超级体育述”中有
分钟的观众称为“超级体育迷”,已知“超级体育述”中有![]() 名女性,若从“超级体育述”中任意选取
名女性,若从“超级体育述”中任意选取![]() 人,求至少有
人,求至少有![]() 名女性观众的概率.
名女性观众的概率.
附: 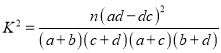 ,
,
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现安排甲乙丙丁戊5名学生分别担任语文、数学、英语、物理、化学学科的科代表,要求甲不当语文科代表,乙不当数学科代表,若丙当物理科代表则丁必须当化学科代表,则不同的选法共有多少种( )
A. 53 B. 67 C. 85 D. 91
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子内装有8张卡片,每张卡片上面写着1个数字,这8个数字各不相同,且奇数有3个,偶数有5个.每张卡片被取出的概率相等.
(Ⅰ)如果从盒子中一次随机取出2张卡片,并且将取出的2张卡片上的数字相加得到一个新数,求所得新数是偶数的概率;
(Ⅱ)现从盒子中一次随机取出1张卡片,每次取出的卡片都不放回盒子,若取出的卡片上写着的数是偶数则停止取出卡片,否则继续取出卡片.设取出了![]() 次才停止取出卡片,求
次才停止取出卡片,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com