
【题目】如图,网格纸上小正方形的边长为1,粗线画出的是某个四面体的三视图,则该四面体的表面积为( ) 
A.8+8 ![]() +4
+4 ![]()
B.8+8 ![]() +2
+2 ![]()
C.2+2 ![]() +
+ ![]()
D.![]() +
+ ![]() +
+ ![]()
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知a为实数,函数f(x)=x2﹣|x2﹣ax﹣2|在区间(﹣∞,﹣1)和(2,+∞)上单调递增,则a的取值范围为( )
A.[1,8]
B.[3,8]
C.[1,3]
D.[﹣1,8]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只药用昆虫的产卵数![]() 与一定范围内的温度
与一定范围内的温度![]() 有关,现收集了该种药用昆虫的6组观测数据如下表:
有关,现收集了该种药用昆虫的6组观测数据如下表:
温度 | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数 | 6 | 11 | 20 | 27 | 57 | 77 |
(1)若用线性回归模型,求![]() 关于
关于![]() 的回归方程
的回归方程![]() (精确到0.1);
(精确到0.1);
(2)若用非线性回归模型求![]() 关
关![]() 的回归方程为
的回归方程为![]() ,且相关指数
,且相关指数![]()
①试与(1)中的线性回归模型相比,用![]() 说明哪种模型的拟合效果更好.
说明哪种模型的拟合效果更好.
②用拟合效果好的模型预测温度为![]() 时该种药用昆虫的产卵数(结果取整数).
时该种药用昆虫的产卵数(结果取整数).
附:一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为 ;相关指数
;相关指数 .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式|x+3|<2x+1的解集为{x|x>m}. (Ⅰ)求m的值;
(Ⅱ)设关于x的方程|x﹣t|+|x+ ![]() |=m(t≠0)有解,求实数t的值.
|=m(t≠0)有解,求实数t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() =(﹣
=(﹣ ![]() sinωx,cosωx),
sinωx,cosωx), ![]() =(cosωx,cosωx),ω>0,记函数f(x)=
=(cosωx,cosωx),ω>0,记函数f(x)= ![]()
![]() ,且f(x)的最小正周期为π.
,且f(x)的最小正周期为π.
(1)求ω的值;
(2)求f(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、N分别是BD和AE的中点,那么![]() ;
;![]() 面CDE;
面CDE;![]() ;
;![]() MN,CE异面其中正确结论的序号是______.
MN,CE异面其中正确结论的序号是______.
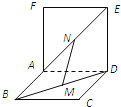
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点. (Ⅰ)证明:SO⊥平面ABC;
(Ⅱ)求二面角A﹣SC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,具有线性相关关系,下表为抽样试验的结果:
转速 | 8 | 10 | 12 | 14 | 16 |
每小时生产有缺点的零件数 | 5 | 7 | 8 | 9 | 11 |
(1)如果![]() 对
对![]() 有线性相关关系,求回归方程;
有线性相关关系,求回归方程;
(2)若实际生产中,允许每小时生产的产品中有缺点的零件最多有1个,那么机器的运转速度应控制在什么范围内?参考公式:![]() ,
,
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com