
本小题满分13分)
如图,A地到火车站共有两条路径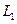 和
和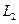 ,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:
,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:
| 时间(分钟) | 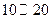 | 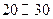 | 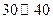 |  | 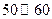 |
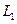 的频率 的频率 | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 |
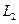 的频率 的频率 | 0 | 0.1 | 0.4 | 0.4 | 0.1 |
科目:高中数学 来源: 题型:
(本小题满分13分)
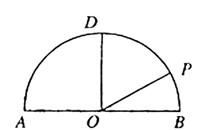
如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,
∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P。
(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)设过点D的直线l与曲线C相交于不同的两点E、F。若△OEF的面积不小于2![]() ,求直线l斜率的取值范围。
,求直线l斜率的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009安徽卷文)(本小题满分13分)
如图,ABCD的边长为2的正方形,直线l与平面ABCD平行,g和F式l上的两个不同点,且EA=ED,FB=FC, ![]() 和
和![]() 是平面ABCD内的两点,
是平面ABCD内的两点,![]() 和
和![]()
![]() 都与平面ABCD垂直,
都与平面ABCD垂直,
(Ⅰ)证明:直线![]() 垂直且平分线段AD:.
垂直且平分线段AD:.
(Ⅱ)若∠EAD=∠EAB=60°,EF=2,求多面
体ABCDEF的体积。
查看答案和解析>>
科目:高中数学 来源:2010年江西省新余一中 宜春中学 高安中学高二上学期第三次阶段考试理科数学卷 题型:解答题
(本小题满分13分)
如图,正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°.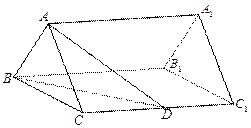
(1)求此正三棱柱的侧棱长;
(2)求平面ABD与平面CBD夹角的余弦;
(3)求点C到平面ABD的距离.
查看答案和解析>>
科目:高中数学 来源:2013届江西省高三10月月考理科数学试卷(解析版) 题型:解答题
(本小题满分13分)如图(甲),在直角梯形ABED中,AB//DE,AB BE,AB
BE,AB CD,且BC=CD,AB=2,F、H、G分别为AC ,AD ,DE的中点,现将△ACD沿CD折起,使平面ACD
CD,且BC=CD,AB=2,F、H、G分别为AC ,AD ,DE的中点,现将△ACD沿CD折起,使平面ACD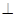 平面CBED,如图(乙).
平面CBED,如图(乙).
(1)求证:平面FHG//平面ABE;
(2)记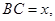
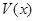 表示三棱锥B-ACE
的体积,求
表示三棱锥B-ACE
的体积,求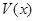 的最大值;
的最大值;
(3)当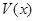 取得最大值时,求二面角D-AB-C的余弦值.
取得最大值时,求二面角D-AB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源:2012届山东省高二下学期期末考试文科数学 题型:解答题
(本小题满分13分)
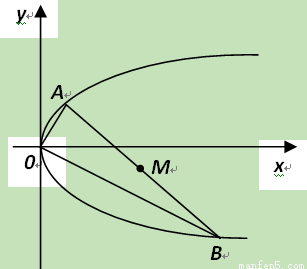
如图,过抛物线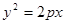 (
( >0)的顶点作两条互相垂直的弦OA、OB。
>0)的顶点作两条互相垂直的弦OA、OB。
⑴设OA的斜率为k,试用k表示点A、B的坐标;
⑵求弦AB中点M的轨迹方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com