
【题目】已知抛物线的方程为![]() :
: ![]() ,过点
,过点![]() 的一条直线与抛物线
的一条直线与抛物线![]() 交于
交于![]() 两点,若抛物线在
两点,若抛物线在![]() 两点的切线交于点
两点的切线交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 的斜率存在,取为
的斜率存在,取为![]() ,取直线
,取直线![]() 的斜率为
的斜率为![]() ,请验证
,请验证![]() 是否为定值?若是,计算出该值;若不是,请说明理由.
是否为定值?若是,计算出该值;若不是,请说明理由.
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x与销售额(单位:百万元)之间有如下对应数据:
如果y与x之间具有线性相关关系.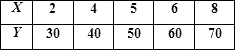
(1)作出这些数据的散点图;
(2)求这些数据的线性回归方程;
(3)预测当广告费支出为9百万元时的销售额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)求圆![]() 的直角坐标方程及弦
的直角坐标方程及弦![]() 的长;
的长;
(2)动点![]() 在圆
在圆![]() 上(不与
上(不与![]() ,
, ![]() 重合),试求
重合),试求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】雾霾天气是一种大气污染状态,PM2.5被认为是造成雾霾天气的“元凶”,PM2.5日均值越小,空气质量越好.国家环境标准设定的PM2.5日均值(微克/立方米)与空气质量等级对应关系如表:
PM2.5日均值 | 0﹣﹣35 | 35﹣﹣75 | 75﹣﹣115 | 115﹣﹣150 | 150﹣﹣250 | 250以上 |
空气质量等级 | 1级 | 2级 | 3级 | 4级 | 5级 | 6级 |
由某市城市环境监测网获得4月份某5天甲、乙两城市的空气质量指数数据,用茎叶图表示,如图所示.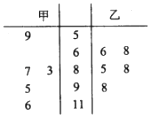
(1)试根据统计数据,分别写出两城区的PM2.5日均值的中位数,并从中位数角度判断哪个城区的空气质量较好?
(2)考虑用频率估计概率的方法,试根据统计数据,估计甲城区某一天空气质量等级为3
(3)分别从甲、乙两个城区的统计数据中任取一个,试求这两城区空气质量等级相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=3ax2+2bx+c,且有a+b+c=0,f(0)>0,f(1)>0.
(Ⅰ)求证:a>0,且﹣2< ![]() <﹣1;
<﹣1;
(Ⅱ)求证:函数y=f(x)在区间(0,1)内有两个不同的零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把边长为2的正方形ABCD沿对角线BD折起并连接AC形成三棱锥C﹣ABD,其正视图、俯视图均为等腰直角三角形(如图所示),则三棱锥C﹣ABD的表面积为 . 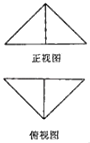
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,A、B、C三点满足 ![]() =
= ![]()
![]() +
+ ![]()
![]() .
.
(1)求证:A、B、C三点共线;
(2)已知A(1,cosx),B(1+cosx,cosx)(0≤x≤ ![]() ),f(x)=
),f(x)= ![]()
![]() ﹣(2m+
﹣(2m+ ![]() )|
)| ![]() |的最小值为﹣
|的最小值为﹣ ![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点 ,
两点 , ![]() 为
为![]() 的中点,且
的中点,且![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() (不与坐标轴垂直)与椭圆
(不与坐标轴垂直)与椭圆![]() 交于
交于![]() 两点,问:在
两点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com