
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
【答案】(1) 乙班平均身高高于甲班. (2) ![]() (3)
(3) ![]()
【解析】
试题分析:本题中“茎是百位和十位”,叶是个位,从图中分析出参与运算的数据,代入相应公式即可解答
试题解析:(1)由茎叶图可知:甲班身高集中于![]() 之间,而乙班身高集中于
之间,而乙班身高集中于![]()
之间,因此乙班平均身高高于甲班.
(2) ![]()
甲班的样本方差为![]()
![]()
(3)设身高为176cm的同学被抽中的事件为A,
从乙班10名同学中抽中两名身高不低于173cm的同学有:(181,173),(181,176)
(181,178),(181,179),(179,173),(179,176),(179,178),(178,173)
(178, 176) ,(176,173)共10个基本事件,而事件A含有4个基本事件;
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修,可供利用的旧墙足够长),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图2所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m, 设利用旧墙的长度为![]() (单位:
(单位: ![]() ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为![]() (单位:元).
(单位:元).

(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)试确定![]() ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与曲线
与曲线![]() 有三个不同的交点.
有三个不同的交点.
(1)求圆![]() 的方程;
的方程;
(2)已知点![]() 是
是![]() 轴上的动点,
轴上的动点, ![]() ,
, ![]() 分别切圆
分别切圆![]() 于
于![]() ,
, ![]() 两点.
两点.
①若![]() ,求
,求![]() 及直线
及直线![]() 的方程;
的方程;
②求证:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2M,N分别是A1B1,A1A的中点。

(1)求![]() 的长度;
的长度;
(2)求cos(![]() ,
,![]() )的值;
)的值;
(3)求证:A1B⊥C1M。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一河南旅游团到安徽旅游.看到安徽有很多特色食品,其中水果类较有名气的有:怀远石榴、砀山梨、徽州青枣等19种,点心类较有名气的有:一品玉带糕、徽墨酥、八公山大救驾等38种,小吃类较有名气的有:符离集烧鸡、无为熏鸭、合肥龙虾等57种.该旅游团的游客决定按分层抽样的方法从这些特产中买6种带给亲朋品尝.
(1)求应从水果类、点心类、小吃类中分别买回的种数;
(2)若某游客从买回的6种特产中随机抽取2种送给自己的父母,
①列出所有可能的抽取结果;
②求抽取的2种特产均为小吃的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解我国各景点在大众中的熟知度,随机对![]() ~
~![]() 岁的人群抽样了
岁的人群抽样了![]() 人,回答问题“我国的“五岳”指的是哪五座名山?”统计结果如下图表.
人,回答问题“我国的“五岳”指的是哪五座名山?”统计结果如下图表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) |
| 0.5 |
第2组 | [25,35) | 18 |
|
第3组[ | [35,45) |
| 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 |
|
![]()
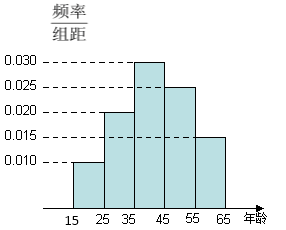
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组各抽取多少人;
组每组各抽取多少人;
(3)在(2)的条件下抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,求所抽取的人中恰好没有第
人,求所抽取的人中恰好没有第![]() 组人的概率.
组人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,平面直角坐标系上的一个动点
,平面直角坐标系上的一个动点![]() 满足
满足![]() .设动点
.设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)点![]() 是曲线
是曲线![]() 上的任意一点,
上的任意一点,![]() 为圆
为圆![]() 的任意一条直径,求
的任意一条直径,求![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过点
,过点![]() 作直线
作直线![]() 与椭圆交于
与椭圆交于![]() 两点.
两点.
(1)若点![]() 平分线段
平分线段![]() ,试求直线
,试求直线![]() 的方程;
的方程;
(2)设与满足(1)中条件的直线![]() 平行的直线与椭圆交于
平行的直线与椭圆交于![]() 两点,
两点,![]() 与椭圆交于点
与椭圆交于点![]() ,
,![]() 与椭圆交于点
与椭圆交于点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《选修4—4:坐标系与参数方程》
已知直线l的参数方程为 (t为参数),若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为ρ=2cos(θ-).
(t为参数),若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为ρ=2cos(θ-).
(1)求直线l的倾斜角和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线l与曲线C交于A,B两点,设点![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com