
【题目】如图1, ![]() ,
, ![]() ,过动点A作
,过动点A作![]() ,垂足D在线段BC上且异于点B,连接AB,沿
,垂足D在线段BC上且异于点B,连接AB,沿![]() 将△
将△![]() 折起,使
折起,使![]() (如图2所示).
(如图2所示).

(1)当![]() 的长为多少时,三棱锥
的长为多少时,三棱锥![]() 的体积最大;
的体积最大;
(2)当三棱锥![]() 的体积最大时,设点
的体积最大时,设点![]() ,
, ![]() 分别为棱
分别为棱![]() ,
, ![]() 的中点,试在棱
的中点,试在棱![]() 上确定一点
上确定一点![]() ,使得
,使得![]()
![]() ,并求
,并求![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(1)![]() 时,三棱锥
时,三棱锥![]() 的体积最大.(2)当
的体积最大.(2)当![]() 时,
时, ![]() .
. ![]() 与平面
与平面![]() 所成角的大小
所成角的大小![]() .
.
【解析】试题分析:(1)设![]() ,则
,则![]() .又
.又![]() ,所以
,所以![]() .由此易将三棱锥
.由此易将三棱锥![]() 的体积表示为
的体积表示为![]() 的函数,通过求函数的最值的方法可求得它的最大值.
的函数,通过求函数的最值的方法可求得它的最大值.
(2)沿![]() 将△
将△![]() 折起后,
折起后, ![]() 两两互相垂直,故可以
两两互相垂直,故可以![]() 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系![]() ,利用空间向量即可找到点N的位置,并求得
,利用空间向量即可找到点N的位置,并求得![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
试题解析:(1)解法1:在如图1所示的△![]() 中,设
中,设![]() ,则
,则![]() .
.
由![]() ,
, ![]() 知,△
知,△![]() 为等腰直角三角形,所以
为等腰直角三角形,所以![]() .
.
由折起前![]() 知,折起后(如图2),
知,折起后(如图2),![]() ,
, ![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() .又
.又![]() ,所以
,所以![]() .于是
.于是
![]()
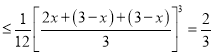 ,
,
当且仅当![]() ,即
,即![]() 时,等号成立,
时,等号成立,
故当![]() ,即
,即![]() 时,三棱锥
时,三棱锥![]() 的体积最大.
的体积最大.
解法2:同解法1,得![]() .
.
令![]() ,由
,由![]() ,且
,且![]() ,解得
,解得![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以当![]() 时,
时, ![]() 取得最大值.
取得最大值.
故当![]() 时,三棱锥
时,三棱锥![]() 的体积最大.
的体积最大.
(2)以![]() 为原点,建立如图a所示的空间直角坐标系
为原点,建立如图a所示的空间直角坐标系![]() .
.
由(1)知,当三棱锥![]() 的体积最大时,
的体积最大时, ![]() ,
, ![]() .
.
于是可得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
且![]() .
.
设![]() ,则
,则![]() .因为
.因为![]() 等价于
等价于![]() ,即
,即
![]() ,故
,故![]() ,
, ![]() .
.
所以当![]() (即
(即![]() 是
是![]() 的靠近点
的靠近点![]() 的一个四等分点)时,
的一个四等分点)时, ![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,由
,由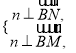 及
及![]() ,
,
得![]() 可取
可取![]() .
.
设![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ,则由
,则由![]() ,
, ![]() ,可得
,可得
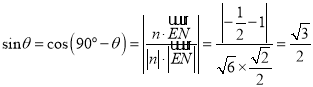 ,即
,即![]() .
.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,则(ⅰ)
,则(ⅰ)![]() ____________.
____________.
(ⅱ)给出下列三个命题:①函数![]() 是偶函数;②存在
是偶函数;②存在![]() ,使得以点
,使得以点![]() 为顶点的三角形是等腰三角形;③存在
为顶点的三角形是等腰三角形;③存在![]() ,使得以点
,使得以点![]() 为顶点的四边形为菱形.
为顶点的四边形为菱形.
其中,所有真命题的序号是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国“雾霾天气”频发,严重影响人们的身体健康.根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
API | 0~50 | 51~100 | 101~150 | 151~200 | 201~250 | 251~300 | >300 |
级别 | Ⅰ | Ⅱ | Ⅲ1 | Ⅲ2 | Ⅳ1 | Ⅳ2 | Ⅴ |
状况 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
|
|
|
|
| |||
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组,得到频率分布直方图如图.
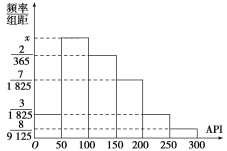
(1)求频率分布直方图中x的值;
(2)计算一年中空气质量分别为良和轻微污染的天数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校高一年级开设![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五门选修课,每位同学须彼此独立地选三课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三课程,其中甲同学必选![]() 课程,不选
课程,不选![]() 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
(Ⅰ)求甲同学选中![]() 课程且乙同学未选中
课程且乙同学未选中![]() 课程的概率.
课程的概率.
(Ⅱ)用![]() 表示甲、乙、丙选中
表示甲、乙、丙选中![]() 课程的人数之和,求
课程的人数之和,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,点
,点![]() 是圆上任意一点,线段
是圆上任意一点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,设动点
,设动点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 两点,
两点, ![]() 为坐标原点,若
为坐标原点,若![]() 的重心恰好在圆
的重心恰好在圆![]() 上,求
上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com