
【题目】已知抛物线E:y2=2px(p>0)的准线与x轴交于点K,过点K作圆(x﹣5)2+y2=9的两条切线,切点为M,N,|MN|=3 ![]()
(1)求抛物线E的方程;
(2)设A,B是抛物线E上分别位于x轴两侧的两个动点,且 ![]() (其中O为坐标原点).
(其中O为坐标原点).
①求证:直线AB必过定点,并求出该定点Q的坐标;
②过点Q作AB的垂线与抛物线交于G,D两点,求四边形AGBD面积的最小值.
【答案】
(1)解:由已知可得K(﹣ ![]() ,0),圆C:(x﹣5)2+y2=9的圆心C(5,0),半径r=3.
,0),圆C:(x﹣5)2+y2=9的圆心C(5,0),半径r=3.
设MN与x轴交于R,由圆的对称性可得|MR|= ![]()
于是|CR|= ![]() ,
,
即有|CK|= ![]() =6,
=6,
即有5+ ![]() =6,解得p=2,则抛物线E的方程为y2=4x
=6,解得p=2,则抛物线E的方程为y2=4x
(2)证明①:设直线AB:x=my+t,A( ![]() ,y1),B(
,y1),B( ![]() ,y2),
,y2),
联立抛物线方程可得y2﹣4my﹣4t=0,
y1+y2=4m,y1y2=﹣4t,
![]() ,即有
,即有 ![]()
![]() +y1y2=
+y1y2= ![]() ,
,
解得y1y2=﹣18或2(舍去),
即﹣4t=﹣18,解得t= ![]() .
.
则有AB恒过定点Q( ![]() ,0);
,0);
②解:由①可得|AB|= ![]() |y2﹣y1|=
|y2﹣y1|= ![]() ,
,
同理|GD|= ![]() ,
,
则四边形AGBD面积S= ![]() |AB||GD|=4
|AB||GD|=4 ![]() ,
,
令m2+ ![]() =μ(μ≥2),则S=4
=μ(μ≥2),则S=4 ![]() 是关于μ的增函数,
是关于μ的增函数,
则当μ=2时,S取得最小值,且为88.
当且仅当m=±1时,四边形AGBD面积的最小值为88
【解析】(1)求得K的坐标,圆的圆心和半径,运用对称性可得MR的长,由勾股定理和锐角的三角函数,可得CK=6,再由点到直线的距离公式即可求得p=2,进而得到抛物线方程;(2)①设出直线方程,联立抛物线方程,运用韦达定理和向量的数量积的坐标表示,化简整理,即可得到定点Q;
②运用弦长公式和四边形的面积公式,换元整理,结合基本不等式,即可求得最小值.


科目:高中数学 来源: 题型:
【题目】(本题满分15分)如图,在四棱锥![]() 中,平面PAD⊥平面ABCD,
中,平面PAD⊥平面ABCD, ![]() ,
,![]() ,E是BD的中点.
,E是BD的中点.

(Ⅰ)求证:EC//平面APD;
(Ⅱ)求BP与平面ABCD所成角的正切值;
(Ⅲ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在(0,+∞)上单调函数,且对x∈(0,+∞),都有f(f(x)﹣lnx)=e+1,则方程f(x)﹣f′(x)=e的实数解所在的区间是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.(1,e)
D.(e,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sin
sin ![]() cos
cos ![]() ﹣2sin2
﹣2sin2 ![]() (ω>0)的最小正周期为3π.
(ω>0)的最小正周期为3π.
(I)求函数f(x)的单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别为角A,B,C所对的边,a<b<c, ![]() a=2csinA,并且f(
a=2csinA,并且f( ![]() A+
A+ ![]() )=
)= ![]() ,求cosB的值.
,求cosB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个同学家开了一个奶茶店,他为了研究气温对热奶茶销售杯数的影响,从一季度中随机选取5天,统计出气温与热奶茶销售杯数,如表:
气温 | 0 | 4 | 12 | 19 | 27 |
热奶茶销售杯数 | 150 | 132 | 130 | 104 | 94 |
(Ⅰ)求热奶茶销售杯数关于气温的线性回归方程![]() (
(![]() 精确到0.1),若某天的气温为
精确到0.1),若某天的气温为![]() ,预测这天热奶茶的销售杯数;
,预测这天热奶茶的销售杯数;
(Ⅱ)从表中的5天中任取两天,求所选取两天中至少有一天热奶茶销售杯数大于130的概率.
参考数据:![]() ,
,![]() .
.
参考公式: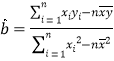 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AA1=AD=a,E为CD上任意一点.
(I)求证:B1E⊥AD1;
(Ⅱ)若CD= ![]() a,是否存在这样的E点,使得AD1与平面B1AE成45°的角?说明理由.
a,是否存在这样的E点,使得AD1与平面B1AE成45°的角?说明理由.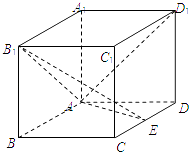
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
![]()
为了研究计算的方便,工作人员将上表的数据进行了处理,![]() 得到下表2:
得到下表2:
![]()
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)通过(1)中的方程,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)用所求回归方程预测到2010年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中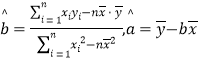 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x﹣1|+|2x﹣3|,x∈R.
(1)若函数f(x)=|2x﹣1|+|2x﹣3|的最小值,并求取的最小值时x的取值范围;
(2)若g(x)= ![]() 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com