
已知曲线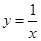 和
和 相交于点A,
相交于点A,
(1)求A点坐标;
(2)分别求它们在A点处的切线方程(写成直线的一般式方程);
(3)求由曲线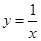 在A点处的切线及
在A点处的切线及 以及
以及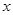 轴所围成的图形面积。(画出草图)
轴所围成的图形面积。(画出草图)
【解析】本试题主要考察了导数的几何意义的运用,以及利用定积分求解曲边梯形的面积的综合试题。先确定切点,然后求解斜率,最后得到切线方程。而求解面积,要先求解交点,确定上限和下限,然后借助于微积分基本定理得到。
科目:高中数学 来源: 题型:
| 16 | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4 |
| 9 |
| 4 |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| π |
| 4 |
| 2π |
| 3 |
| x2 |
| 36 |
| y2 |
| 16 |
|
查看答案和解析>>
科目:高中数学 来源:2013届吉林省高二下学期期初考试理科数学试卷(解析版) 题型:解答题
已知曲线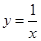 和
和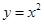 相交于点A,
相交于点A,
(1)求A点坐标;
(2)分别求它们在A点处的切线方程(写成直线的一般式方程);
(3)求由曲线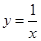 在A点处的切线及
在A点处的切线及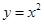 以及
以及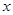 轴所围成的图形面积。(画出草图)
轴所围成的图形面积。(画出草图)
【解析】本试题主要考察了导数的几何意义的运用,以及利用定积分求解曲边梯形的面积的综合试题。先确定切点,然后求解斜率,最后得到切线方程。而求解面积,要先求解交点,确定上限和下限,然后借助于微积分基本定理得到。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com