
分析 (1)化简集合M、N,根据差集的定义写出M-N即可;
(2)化简集合A,根据A-B=∅得出A⊆B,讨论a的取值,列出对应的不等式,求出a的取值范围即可.
解答 解:(1)集合M={{x|y=$\sqrt{2x-1}$}={x|2x-1≥0}={x|x≥$\frac{1}{2}$},
N={y|y=1-x2}={y|y≤1},
M-N={x|x>1};
(2)集合A={x|0<ax-1≤5}={x|1<ax≤6},
B=$\left\{{y|-\frac{1}{2}<y≤2}\right\}$,
且A-B=∅,
∴A⊆B;
当a=0时,不满足题意;
当a>0时,A={x|$\frac{1}{a}$<x≤$\frac{6}{a}$},应满足$\left\{\begin{array}{l}{\frac{1}{a}>-\frac{1}{2}}\\{\frac{6}{a}≤2}\\{a>0}\end{array}\right.$,
解得a≥3;
当a<0时,A={x|$\frac{6}{a}$≤x<$\frac{1}{a}$},应满足$\left\{\begin{array}{l}{\frac{6}{a}>-\frac{1}{2}}\\{\frac{1}{a}≤2}\\{a<0}\end{array}\right.$,
解得a<-12;
综上,a的取值范围是a<-12或a≥3.
点评 本题考查了集合的定义与应用问题,是综合性题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,底面ABC为等边三角形,CC1=2AC=2.
如图,在直三棱柱ABC-A1B1C1中,底面ABC为等边三角形,CC1=2AC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
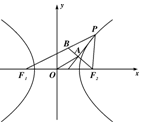 已知F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P在双曲线上且不与顶点重合,过F2作∠F1PF2的角平分线的垂线,垂足为A.若|OA|=b,则该双曲线的离心率为( )
已知F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P在双曲线上且不与顶点重合,过F2作∠F1PF2的角平分线的垂线,垂足为A.若|OA|=b,则该双曲线的离心率为( )| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | 160 | C. | $-\frac{5}{2}$ | D. | -160 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | $(-\frac{1}{e},2{e^2})$ | C. | (0,2e2) | D. | $(-\frac{1}{e},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com