
【题目】选修4-5:不等式选讲
已知函数![]() ,
,![]() .
.
(1)当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() ;
;
(2)若对任意![]() ,都存在
,都存在![]() ,使得不等式
,使得不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】过抛物线![]() :
:![]() 的焦点
的焦点![]() 的直线
的直线![]() (倾斜角为锐角)交抛物线于
(倾斜角为锐角)交抛物线于![]() ,
,![]() 两点,若
两点,若![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() 并延长交抛物线
并延长交抛物线![]() 于点
于点![]() ,已知
,已知![]() ,则直线
,则直线![]() 的斜率是( )
的斜率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬民族古典文化,市电视台举行古诗词知识竞赛,某轮比赛由节目主持人随机从题库中抽取题目让选手抢答,回答正确将给该选手记正10分,否则记负10分.根据以往统计,某参赛选手能答对每一个问题的概率均为![]() ;现记“该选手在回答完
;现记“该选手在回答完![]() 个问题后的总得分为
个问题后的总得分为![]() ”.
”.
(1)求![]() 且
且![]() (
(![]() )的概率;
)的概率;
(2)记![]() ,求
,求![]() 的分布列,并计算数学期望
的分布列,并计算数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某小区居民的“幸福度”。现从所有居民中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶),若幸福度分数不低于8.5分,则称该人的幸福度为“幸福”。

(1)求从这16人中随机选取3人,至少有2人为“幸福”的概率;
(2)以这16人的样本数据来估计整个小区的总体数据,若从该小区(人数很多)任选3人,记![]() 表示抽到“幸福”的人数,求
表示抽到“幸福”的人数,求![]() 的分布列及数学期望和方差。
的分布列及数学期望和方差。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理过程是演绎推理的是( )
A. 某校高三有8个班,1班有51人,2班有53人,3班有52人,由此推测各班人数都超过50人
B. 由三角形的性质,推测空间四面体的性质
C. 平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分
D. 在数列![]() 中,
中,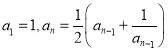 ,可得
,可得![]() ,由此归纳出
,由此归纳出![]() 的通项公式
的通项公式![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1,当f(x)+f(x-8)≤2时,x的取值范围是( )
A.(8,+∞)B.(8,9]C.[8,9]D.(0,8)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类比平面内正三角形的“三边相等,三内角相等”的性质,可推出正四面体的下列性质,你认为比较恰当的是( )
①各棱长相等,同一顶点上的任两条棱的夹角都相等;
②各个面都是全等的正三角形,相邻两个面所成的二面角都相等;
③各面都是面积相等的三角形,同一顶点上的任两条棱的夹角都相等.
A. ①B. ②C. ①②③D. ③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com