
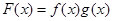 是
是 上的奇函数,当
上的奇函数,当 时,
时, ,且
,且 ,则不等式
,则不等式 的解集是( )
的解集是( )A. | B. |
C. | D. |
科目:高中数学 来源:不详 题型:解答题
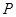 (元)与时间
(元)与时间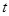 (天)所组成的有序数对
(天)所组成的有序数对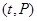 落在下图中的两条线段上,该股票在30天内的日交易量
落在下图中的两条线段上,该股票在30天内的日交易量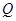 (万股)与时间
(万股)与时间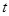 (天)的部分数据如下表所示.
(天)的部分数据如下表所示.
| 第t天 | 4 | 10 | 16 | 22 |
| Q(万股) | 36 | 30 | 24 | 18 |
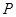 (元)与时间
(元)与时间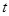 (天)所满足的函数关系式;
(天)所满足的函数关系式;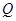 (万股)与时间
(万股)与时间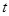 (天)的一次函数关系式;
(天)的一次函数关系式; (万元)表示该股票日交易额,写出
(万元)表示该股票日交易额,写出 关于
关于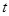 的函数关系式,并求这30天中第几天日交易额最大,最大值为多少?
的函数关系式,并求这30天中第几天日交易额最大,最大值为多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
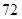 万元建起一座汽车零件加工厂,第一年各种经费
万元建起一座汽车零件加工厂,第一年各种经费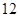 万元,以后每年增加
万元,以后每年增加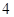 万元,每年的产品销售收入
万元,每年的产品销售收入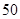 万元.
万元.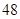 万元出售该厂;
万元出售该厂;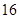 万元出售该厂.
万元出售该厂.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
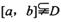 和常数c,使得对任意x1
和常数c,使得对任意x1 ,都有
,都有 ,且对任意x2
,且对任意x2 D,当
D,当 时,
时, 恒成立,则称函数f(x)为区间D上的“平顶型”函数.给出下列说法:
恒成立,则称函数f(x)为区间D上的“平顶型”函数.给出下列说法: 为R上的“平顶型”函数;
为R上的“平顶型”函数; 时,函数,
时,函数, 是区间
是区间 上的“平顶型”函数.
上的“平顶型”函数.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com