
【题目】已知![]() .
.
(Ⅰ)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,证明:
,证明:![]() ,
,![]() 恒成立.
恒成立.
【答案】见解析
【解析】(Ⅰ)![]() .
.
由函数![]() 在
在![]() 上单调递增,可得
上单调递增,可得![]() 在
在![]() 上恒成立,
上恒成立,
即![]() ,得
,得![]() . -----------------2分
. -----------------2分
记![]() (
(![]() ),则
),则![]() .
.
当![]() 时,
时,![]() ,函数单调递减;当
,函数单调递减;当![]() 时,
时,![]() ,函数单调递增.
,函数单调递增.
所以![]() . -----------------5分
. -----------------5分
所以实数![]() 的取值范围为
的取值范围为![]() . ---------------------------6分
. ---------------------------6分
(Ⅱ)设![]() .
.
则![]() ,
,
记![]() ,则
,则![]() ,
,
故当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增. ------------9分
单调递增. ------------9分
又![]() ,
,![]() ,所以
,所以![]() ,使得
,使得![]() ,即
,即![]() .
.
所以当![]() 时,
时,![]() ,函数单调递增;
,函数单调递增;
当![]() 时,
时,![]() ,函数单调递减;
,函数单调递减;
当![]() 时,
时,![]() ,函数单调递增.
,函数单调递增.
而![]() ,
,
所以![]() 时,
时,![]() ,即
,即![]() 恒成立. -----------------13分
恒成立. -----------------13分
【命题意图】本题考查导数与函数的单调性、不等式的证明等,考查基本的逻辑推理能力、运算能力以及数学应用意识等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=xlnx-a(x-1)2-x,g(x)=lnx-2a(x-1),其中常数a∈R.
(Ⅰ)讨论g(x)的单调性;
(Ⅱ)当a>0时,若f(x)有两个零点x1,x2(x1<x2),求证:在区间(1,+∞)上存在f(x)的极值点x0,使得x0lnx0+lnx0-2x0>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品x(百台),总成本为C(x)(万元),其中固定成本为2万元,每生产1百台,成本增加1万元,销售收入 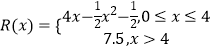 (万元),假定该产品产销平衡.
(万元),假定该产品产销平衡.
(1)若要该厂不亏本,产量x应控制在什么范围内?
(2)该厂年产多少台时,可使利润最大?
(3)求该厂利润最大时产品的售价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种产品,第一年投入资金1000万元,出售产品收入40万元,预计以后每年的投入资金是上一年的一半,出售产品所得收入比上一年多80万元,同时,当预计投入的资金低于20万元时,就按20万元投入,且当年出售产品收入与上一年相等.
(1)求第![]() 年的预计投入资金与出售产品的收入;
年的预计投入资金与出售产品的收入;
(2)预计从哪一年起该公司开始盈利?(注:盈利是指总收入大于总投入)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com