
【题目】设函数![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)求![]() 值;
值;
(2)若![]() ,
,![]() 为自然对数的底数,求证:当
为自然对数的底数,求证:当![]() 时,
时,![]() ;
;
(3)若函数![]() 为
为![]() 上的单调函数,求实数
上的单调函数,求实数![]() 的取值范围.
的取值范围.
【答案】见解析
【解析】(1)依题意![]() .……………2分
.……………2分
(2)记![]() ,则
,则![]() ,
,
设![]() ,则当
,则当![]() 时
时![]() ,因此函数
,因此函数![]() 在
在![]() 上是单调增函数,且
上是单调增函数,且![]() ,
,
所以由零点存在定理知,![]() 在
在![]() 上存在唯一的零点
上存在唯一的零点![]() ,……………5分
,……………5分
令![]() 得
得![]() ,
,
列表:
|
|
|
|
|
|
|
|
| ↘ | 极小值 | ↗ |
所以![]() ,故
,故![]() ……………8分
……………8分
(3)依题意,![]() ,记
,记![]() .
.
![]() 当
当![]() 时,
时,![]()
①若![]() 为
为![]() 上的单调增函数,则
上的单调增函数,则![]() ,即
,即![]() 在
在![]() 上恒成立
上恒成立
因为![]() 为
为![]() 上的单调增函数
上的单调增函数
所以![]() ,从而
,从而![]() ,舍去. ……………10分
,舍去. ……………10分
②若![]() 为
为![]() 上的单调减函数,则
上的单调减函数,则![]() ,即
,即![]() 在
在![]() 上恒成立
上恒成立
因为![]() ,
,
所以![]() 在
在![]() 上不恒成立,舍去. ……………12分
上不恒成立,舍去. ……………12分
![]() 当
当![]() 时,
时,![]()
①若![]() 为
为![]() 上的单调增函数,则
上的单调增函数,则![]() ,即
,即![]() 在
在![]() 上恒成立
上恒成立
由![]() 得
得![]() ,
,
列表:
|
|
|
|
| + | 0 | - |
| ↗ | 极大值 | ↘ |
所以![]()
所以![]() ,即
,即![]() ,故
,故![]() ……………14分
……………14分
②若![]() 为
为![]() 上的单调减函数,则
上的单调减函数,则![]() ,即
,即![]() 在
在![]() 上恒成立
上恒成立
由![]() ①知,当
①知,当![]() 时,
时,![]() ;当
;当![]() ,
,![]()
所以![]() ,不成立,舍去
,不成立,舍去
综上,![]() ……………16分
……………16分
备注:由函数图象能得出若单调必递增(因为图象交点左侧y小于0,右侧y大于0),可减少对![]() 的讨论.
的讨论.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在圆柱中,A,B,C,D是底面圆的四等分点,O是圆心,A1A,B1B,C1C与底面ABCD垂直,底面圆的直径等于圆柱的高.
(Ⅰ)证明:BC⊥AB1;
(Ⅱ)(ⅰ)求二面角A1 - BB1 - D的大小;
(ⅱ)求异面直线AB1和BD所成角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查“五一”小长假出游选择“有水的地方”是否与性别有关,现从该市“五一”出游旅客中随机抽取500人进行调查,得到如下2×2列联表:(单位:人)
选择“有水的地方” | 不选择“有水的地方” | 合计 | |
男 | 90 | 110 | 200 |
女 | 210 | 90 | 300 |
合计 | 300 | 200 | 500 |
(Ⅰ)据此样本,有多大的把握认为选择“有水的地方”与性别有关;
(Ⅱ)若以样本中各事件的频率作为概率估计全市“五一”所有出游旅客情况,现从该市的全体出游旅客(人数众多)中随机抽取3人,设3人中选择“有水的地方”的人数为随机变量X,求随机变量X的数学期望和方差.
附临界值表及参考公式:
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,n=a+b+c+d.
,n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|,g(x)=x+1.
(1)若a=1,求不等式f(x)≤1的解集;
(2)对任意的x∈R,f(x)+|g(x)|≥a2+2a(a>0)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为ρsin(θ+![]() )=
)=![]() ,曲线C的参数方程为
,曲线C的参数方程为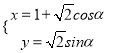 (α为参数).
(α为参数).
(1)求直线l的普通方程;
(2)若P是曲线C上的动点,求点P到直线l的最大距离及点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区为丰富居民节日活动,组织了“迎新春”象棋大赛,已知报名的选手情况统计如下表:
组别 | 男 | 女 | 总计 |
中年组 |
|
| 91 |
老年组 | 16 |
|
|
已知中年组女性选手人数是仅比老年组女性选手人数多2人.若对中年组和老年组分别利用分层抽样的方法抽取部分报名者参加比赛,已知老年组抽取了5人,其中女性3人,中年组抽取了7人.
(Ⅰ)求表格中的数据![]() ;
;
(Ⅱ)若从选出的中年组的选手中随机抽取两名进行比赛,求至少有一名女性选手的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一企业从某条生产线上随机抽取30件产品,测量这些产品的某项技术指标值![]() ,得到如下的频数分布表:
,得到如下的频数分布表:
|
|
|
|
|
频数 | 2 | 6 | 18 | 4 |
(I)估计该技术指标值的平均数和众数(以各组区间的中点值代表该组的取值);
(II) 若![]() 或
或![]() ,则该产品不合格,其余的是合格产品,从不合格的产品中随机抽取2件,求抽取的2件产品中技术指标值小于
,则该产品不合格,其余的是合格产品,从不合格的产品中随机抽取2件,求抽取的2件产品中技术指标值小于![]() 的产品恰有1件的概率.
的产品恰有1件的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com