练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．从装有4个红球和3个黑球的口袋内任取3个球，那么互斥而不对立的事件是（　　）
    A．至少有一个红球与都是黑球B．至少有一个红球与恰有一个黑球
    C．至少有一个红球与至少有一个黑球D．恰有一个红球与恰有两个红球

    分析 分析出从装有4个红球和3个黑球的口袋内任取3个球的所有不同的情况，然后利用互斥事件和对立事件的概念逐一核对四个选项即可得到答案

    解答 解：从装有4个红球和3个黑球的口袋内任取3个球，不同的取球情况共有以下几种：
    3个球全是红球；2个红球1个黑球；1个红球2个黑球；3个球全是黑球．
    选项A中，至少有一个红球与都是黑球”不能同时发生，但一定会有一个发生；这两个事件是对立事件，故不正确；
    选项B中，至少有一个红球与恰有一个黑球”可以同时发生，如：2个红球1个黑球，不是互斥事件，故不正确；
    选项C中，“至少有一个红球”与事件“至少有一个黑球”可以同时发生，例如“2个红球1个黑球”与“1个红球2个黑球”；不是互斥事件，故不正确；
    选项D中，恰有一个红球与恰有两个红互斥不对立．
    故选：D

    点评 本题考查了互斥事件和对立事件，关键是对概念的理解，是基础的概念题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    9．若$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-1，-2），$\overrightarrow{c}$=（2，1），则（$\overrightarrow{a}$•$\overrightarrow{b}$）$\overrightarrow{c}$=（-16，-8），$\overrightarrow{a}$（$\overrightarrow{b}$•$\overrightarrow{c}$）=（-8，-12）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知：a=$\root{3}{4}$+$\root{3}{2}$+$\root{3}{1}$，那么$\frac{3}{a}$+$\frac{3}{{a}^{2}}$+$\frac{1}{{a}^{3}}$=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．城市公交车的数量若太多则容易造成资源的浪费；若太少又难以满足乘客需求．某市公交公司在某站台的60名候车乘客中随机抽取15人，将他们的候车时间作为样本分成5组，如下表所示（单位：分钟）．
    组别一二三四五
    候车时间[0，5）[5，10）[10，15）[15，20）[20，25]
    人数2642l
    （I）估计这60名乘客中候车时间少于10分钟的人数；
    （II）若从上表第三、四组的6人中任选2人作进一步的调查．
    ①列出所有可能的结果；
    ②求抽到的两人恰好来自不同组的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知实系数多项式f（x）=x4+ax3+bx2+cx+d满足f（1）=2，f（2）=4，f（3）=6，则f（0）+f（4）的所有可能值集合为{32}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．下列结论正确的是（　　）
    A．当x＞0且x≠1时，lgx+$\frac{1}{lgx}$≥2B．2x+2-x≥2
    C．当x≥2时，x+$\frac{1}{x}$的最小值2D．当x＞0时，sinx+$\frac{1}{sinx}$≥2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．淘宝卖家在某商品的所有买家中，随机选择男女买家各50名进行调查，他们的评分等级如表：
    评分等级[0，1]（1，2]（2，3]（3，4]（4，5]
    女（人数）2792012
    男（人数）3918128
    规定：评分等级在[0，3]内为不满意该商品，在（3，5]内为满意该商品．完成下列2×2列联表并帮助卖家判断：能否在犯错误的概率不超过0.05的前提下认为满意该商品与性别有关系？
    满意该商品不满意该商品总计
    女321850
    男203050
    总计5248100
    参考数据：
    P（K2≥k）0.150.100.050.0250.0100.0050.001
    k2.0722.7063.8415.0246.6357.87910.828
    （参考公式：K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

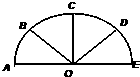    8．如图，在以AE=2为直径的半圆周上，B，C，D分别为弧AE的四等分点．
    （1）以O为起点，从A，B，C，D，E这5个点中任取一点为终点得到一个向量$\overrightarrow{a}$，求满足$\overrightarrow{a}$在$\overrightarrow{OA}$上的射影为正的概率；
    （2）以O为起点，从A，B，C，D，E这5个点中任取两点分别为终点得到两个向量，求这两个向量垂直的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知△ABC的顶点A（5，1），AB边上的中线CM所在的直线方程为2x-y-5=0，AC边上的高BH所在的直线方程为x-2y-5=0，
    （1）求直线AC的方程；
    （2）求点B的坐标（x0，y0）；
    （3）求△ABC的面积．

    查看答案和解析>>

    同步练习册答案