
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1. 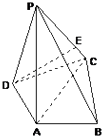
(1)求二面角A﹣PB﹣C的余弦值.
(2)在线段CP上是否存在一点E,使得DE⊥PB,若存在,求线段CE的长度,不存在,说明理由.
【答案】
(1)解:以A为坐标原点,以AB,AC,AP为坐标轴建立空间直角坐标系,
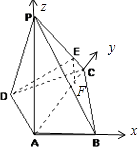
则P(0,0,2),A(0,0,0),B(1,0,0),C(0,2,0),D(﹣ ![]() ,
, ![]() ,0).
,0).
∴ ![]() =(0,2,﹣2),
=(0,2,﹣2), ![]() =(1,0,﹣2),
=(1,0,﹣2), ![]() =(0,2,0).
=(0,2,0).
显然 ![]() =(0,2,0)为平面PAB的法向量.
=(0,2,0)为平面PAB的法向量.
设平面PBC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 ![]() ,
, ![]() =0,
=0,
∴ ![]() ,令z=1,得
,令z=1,得 ![]() =(2,1,1).
=(2,1,1).
∴ ![]() =2,|
=2,| ![]() |=
|= ![]() ,|
,| ![]() |=2.
|=2.
∴cos< ![]() ,
, ![]() >=
>= 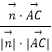 =
= ![]() .
.
∴二面角A﹣PB﹣C的余弦值为 ![]()
(2)解:过E作EF⊥AC于F,∴EF∥PA,∴EF=FC.
设EF=h,则E(0,2﹣h,h).
∴ ![]() =(
=( ![]() ,
, ![]() -h,h),
-h,h), ![]() =(1,0,﹣2).
=(1,0,﹣2).
∵DE⊥PB,∴ ![]() =
= ![]() ﹣2h=0,解得h=
﹣2h=0,解得h= ![]() .
.
∴CE= ![]() h=
h= ![]() .
.
【解析】(1)以A为原点建立空间直角坐标系,求出平面PAB和平面PBC的法向量,则法向量的夹角与二面角的大小相等或互补;(2)作EF⊥AC于F,则EF=FC,设EF=h,求出E点坐标得出 ![]() 的坐标,令
的坐标,令 ![]() =0解出h,从而得出CE.
=0解出h,从而得出CE.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,并且满足
,并且满足![]() ,
, ![]() .
.
(1)求数列![]() 通项公式;
通项公式;
(2)设![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证: ![]() .
.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】试题分析:(1)根据题意得到![]() ,
, ![]() ,两式做差得到
,两式做差得到![]() ;(2)根据第一问得到
;(2)根据第一问得到![]() ,由错位相减法得到前n项和,进而可证和小于1.
,由错位相减法得到前n项和,进而可证和小于1.
解析:
(1)∵![]()
当![]() 时,
时, ![]()
当![]() 时,
时, ![]() ,即
,即![]()
∴数列![]() 时以
时以![]() 为首项,
为首项, ![]() 为公差的等差数列.
为公差的等差数列.
∴![]() .
.
(2)∵![]()
∴![]() ①
①
![]() ②
②
由①![]() ②得
②得
![]()
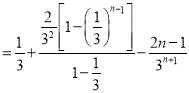
![]()
∴![]()
点睛:这个题目考查的是数列通项公式的求法及数列求和的常用方法;数列通项的求法中有常见的已知![]() 和
和![]() 的关系,求
的关系,求![]() 表达式,一般是写出
表达式,一般是写出![]() 做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等.
做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等.
【题型】解答题
【结束】
22
【题目】已知![]() ,
, ![]() 分别是椭圆
分别是椭圆![]() :
: ![]() (
(![]() )的左、右焦点,
)的左、右焦点, ![]() 是椭圆
是椭圆![]() 上的一点,且
上的一点,且![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,
, ![]() ,椭圆
,椭圆![]() 上存在点
上存在点![]() ,使得以
,使得以![]() ,
, ![]() 为邻边的四边形
为邻边的四边形![]() 为平行四边形(
为平行四边形(![]() 为坐标原点).
为坐标原点).
(ⅰ)求实数![]() 与
与![]() 的关系;
的关系;
(ⅱ)证明:四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上的点到它的两个焦的距离之和为
上的点到它的两个焦的距离之和为![]() ,以椭圆
,以椭圆![]() 的短轴为直径的圆
的短轴为直径的圆![]() 经过这两个焦点,点
经过这两个焦点,点![]() ,
, ![]() 分别是椭圆
分别是椭圆![]() 的左、右顶点.
的左、右顶点.
(![]() )求圆
)求圆![]() 和椭圆
和椭圆![]() 的方程.
的方程.
(![]() )已知
)已知![]() ,
, ![]() 分别是椭圆
分别是椭圆![]() 和圆
和圆![]() 上的动点(
上的动点(![]() ,
, ![]() 位于
位于![]() 轴两侧),且直线
轴两侧),且直线![]() 与
与![]() 轴平行,直线
轴平行,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .求证:
.求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设实数x,y满足不等式组  ,(2,1)是目标函数z=﹣ax+y取最大值的唯一最优解,则实数a的取值范围是( )
,(2,1)是目标函数z=﹣ax+y取最大值的唯一最优解,则实数a的取值范围是( )
A.(0,1)
B.(0,1]
C.(﹣∞,﹣2)
D.(﹣∞,﹣2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答
(1)在公比为2的等比数列{an}中,a2与a5的等差中项是9 ![]() .求a1的值;
.求a1的值;
(2)若函数y=a1sin( ![]() φ),0<φ<π的一部分图象如图所示,M(﹣1,a1),N(3,﹣a1)为图象上的两点,设∠MON=θ,其中O为坐标原点,0<θ<π,求cos(θ﹣φ)的值.
φ),0<φ<π的一部分图象如图所示,M(﹣1,a1),N(3,﹣a1)为图象上的两点,设∠MON=θ,其中O为坐标原点,0<θ<π,求cos(θ﹣φ)的值. 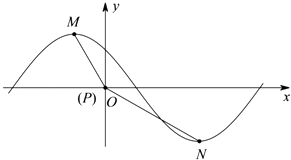
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种出口产品的关税税率![]() ,市场价格
,市场价格![]() (单位:千元)与市场供应量
(单位:千元)与市场供应量![]() (单位:万件)之间近似满足关系式:
(单位:万件)之间近似满足关系式:![]() ,其中
,其中![]() 、
、![]() 均为常数.当关税税率为
均为常数.当关税税率为![]() 时,若市场价格为5千元,则市场供应量约为1万件;当关税税率为
时,若市场价格为5千元,则市场供应量约为1万件;当关税税率为![]() 时,若市场价格为7千元,则市场供应量约为2万件.
时,若市场价格为7千元,则市场供应量约为2万件.
(1)试确定![]() 、
、![]() 的值;
的值;
(2)市场需求量![]() (单位:万件)与市场价格
(单位:万件)与市场价格![]() 近似满足关系式:
近似满足关系式:![]() .当
.当![]() 时,市场价格称为市场平衡价格.当市场平衡价格不超过4千元时,试确定关税税率的最大值.
时,市场价格称为市场平衡价格.当市场平衡价格不超过4千元时,试确定关税税率的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=﹣1,|an﹣an﹣1|=2n﹣1(n∈N,n≥2),且{a2n﹣1}是递减数列,{a2n}是递增数列,则a2016= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由形状为长方形A1B1C1D1的休闲区和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米(如图所示).

(1)若设休闲区的长和宽的比![]() =x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
=x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,则休闲区A1B1C1D1的长和宽该如何设计?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com