练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，一条河的两岸平行，河的宽度d=600m，一艘客船从码头A出发匀速驶往河对岸的码头B.已知|AB|=1km，水流速度为2km/h, 若客船行驶完航程所用最短时间为6分钟，则客船在静水中的速度大小为（ ）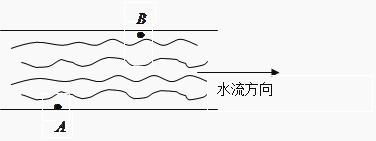

    A.8km/h
    B.km/h
    C.km/h
    D.10km/h

    【答案】B
    【解析】河宽0.6km, |AB|=1km，船航行的和速度为 ， 和速度在垂直河岸的方向上的分速度为,沿河岸方向的分速度为,因为水速为2，所以穿在静水中的速度
    正确理解本题中船的航行方向即速度方向是前提条件，然后将速度分解到河流方向与垂直河岸方向，因此就能得到静水中沿河流方向与垂直河流方向的分速度各为多少，从而求得静水中的航速，学生对本题的题意理解有一定困难。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知向量 =（cosα，sinα）， =（cosβ，sinβ），0＜β＜α＜π．
    （1）若| ﹣ |= ，求证： ⊥ ；
    （2）设c=（0，1），若 + =c，求α，β的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】两城相距,在两城之间距城处建一核电站给两城供电,为保证城市安全,核电站距城市距离不得小于 .已知供电费用等于供电距离的平方与供电量(亿度)之积的倍,若城供电量为每月20亿度,城供电量为每月10亿度.

    （1）把月供电总费用表示成的函数;

    （2）核电站建在距城多远,才能使供电总费用最少?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司研发出一款新产品，批量生产前先同时在甲、乙两城市销售30天进行市场调查.调查结果发现：甲城市的日销售量 与天数的对应关系服从图①所示的函数关系；乙城市的日销售量与天数的对应关系服从图②所示的函数关系；每件产品的销售利润与天数的对应关系服从图③所示的函数关系，图①是抛物线的一部分.

    图①，图②，图③

    （1）设该产品的销售时间为，日销售利润为，求的解析式；

    （2）若在30天的销售中，日销售利润至少有一天超过2万元，则可以投入批量生产，该产品是否可以投入批量生产，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2﹣2（a+2）x+a2 ， g（x）=﹣x2+2（a﹣2）x﹣a2+8．设H1（x）=max{f（x），g（x）}，H2（x）=min{f（x），g（x）}，（其中max{p，q}表示p，q中的较大值，min{p，q}表示p，q中的较小值）．记H1（x）的最小值为A，H2（x）的最大值为B，则A﹣B=（ ）
    A.a2﹣2a﹣16
    B.a2+2a﹣16
    C.﹣16
    D.16

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有下列说法： ①线性回归分析就是由样本点去寻找一条直线，使之贴近这些样本点的数学方法；②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示；③通过回归方程 ，可以估计和观测变量的取值和变化趋势；④因为由任何一组观测值都可以求得一个线性回归方程，所以没有必要进行相关性检验.其中正确命题的个数是（ ）
    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】海上某货轮在A处看灯塔B在货轮的北偏东75°，距离为12海里；在A处看灯塔C在货轮的北偏西30°，距离为8海里；货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°．（要画图）
    （1）A处与D处之间的距离；
    （2）灯塔C与D处之间的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 函数f（x）=x3+（m﹣4）x2﹣3mx+（n﹣6）x∈R的图象关于原点对称，其中m，n为实常数．
    （1）求m，n的值；
    （2）试用单调性的定义证明：f（x）在区间[﹣2，2]上是单调函数；
    （3）当﹣2≤x≤2 时，不等式f（x）≥（n﹣logma）logma恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2﹣2x，g（x）=ax+2（a＞0），且对任意的x1∈[﹣1，2]，都存在x2∈[﹣1，2]，使f（x2）=g（x1），则实数a的取值范围是（ ）
    A.[3，+∞）
    B.（0，3]
    C.[ ，3]
    D.（0， ]

    查看答案和解析>>

    同步练习册答案