
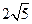 ,设这条最短路线与CC1的交
,设这条最短路线与CC1的交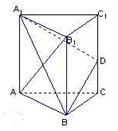
 (2)在平面A1BD内存在过点D的直线与平面ABC平行
(2)在平面A1BD内存在过点D的直线与平面ABC平行  ,则B2C=AC=AA1=
,则B2C=AC=AA1= ,
,
 ,
, 解得
解得 ,……………………4分
,……………………4分 ∴
∴ ……………………………………6分
……………………………………6分 ……………………………7分
……………………………7分 平面
平面 ,
, 平面
平面 ∴
∴ 平面
平面 ,
, ≌
≌ ≌
≌
 ∴
∴ ……………………………11分
……………………………11分 ∴
∴ 平面A1ABB1 ……………………………13分
平面A1ABB1 ……………………………13分 平面A1BD ∴平面A1BD⊥平面A1ABB1 ……………………………………14分
平面A1BD ∴平面A1BD⊥平面A1ABB1 ……………………………………14分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
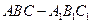 中,AB=4,
中,AB=4,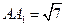 ,点D是BC的中点,
,点D是BC的中点,
 E。
E。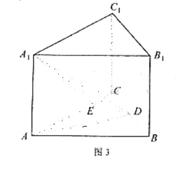
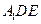
 平面
平面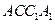 ;
;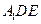 所成角的正弦值。
所成角的正弦值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
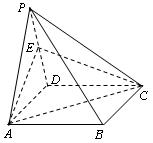
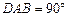 , AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
, AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点. ,
,
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
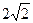 ,M为BC的中点
,M为BC的中点查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
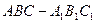 的底面边长是2,D是侧棱
的底面边长是2,D是侧棱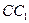 的中点,平面ABD和平面
的中点,平面ABD和平面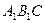 的交线为MN.
的交线为MN.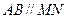 ;
;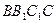 所成的角为
所成的角为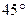 ,试求二面角
,试求二面角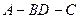 的大小.
的大小.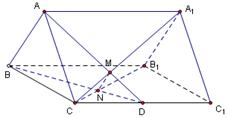
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
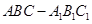 的侧面
的侧面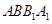 是圆柱的轴截面,
是圆柱的轴截面,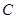 是圆柱底面圆周上不与
是圆柱底面圆周上不与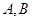 重合一个点。
重合一个点。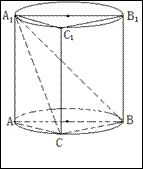
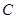 如何运动,平面
如何运动,平面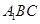
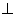 平面
平面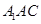 ;
;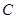 是弧
是弧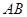 的中点时,求四棱锥
的中点时,求四棱锥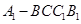 与圆柱的体积比。
与圆柱的体积比。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
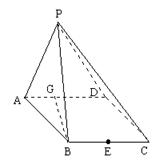
 如图,PC⊥平面ABC,PM∥CB,∠ACB=120°,PM=AC=1,BC=2,异面直线AM与直线PC所成的角为60°.
如图,PC⊥平面ABC,PM∥CB,∠ACB=120°,PM=AC=1,BC=2,异面直线AM与直线PC所成的角为60°.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com