
【题目】某同学研究曲线![]() 的性质,得到如下结论:①
的性质,得到如下结论:①![]() 的取值范围是
的取值范围是![]() ;②曲线
;②曲线![]() 是轴对称图形;③曲线
是轴对称图形;③曲线![]() 上的点到坐标原点的距离的最小值为
上的点到坐标原点的距离的最小值为![]() . 其中正确的结论序号为( )
. 其中正确的结论序号为( )
A.①②B.①③C.②③D.①②③
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的极值;
的极值;
(2)问:是否存在实数![]() ,使得
,使得![]() 有两个相异零点?若存在,求出
有两个相异零点?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某数学小组到进行社会实践调查,了解到某公司为了实现1000万元利润目标,准备制定激励销售人员的奖励方案:在销售利润超过10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%.同学们利用函数知识,设计了如下的函数模型,其中符合公司要求的是(参考数据:![]() ,
,![]() )( )
)( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
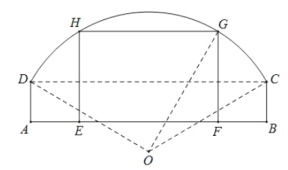
【题目】如下图所示,某窑洞窗口形状上部是圆弧![]() ,下部是一个矩形
,下部是一个矩形![]() ,圆弧
,圆弧![]() 所在圆的圆心为O,经测量
所在圆的圆心为O,经测量![]() 米,
米,![]() 米,
米,![]() ,现根据需要把此窑洞窗口形状改造为矩形
,现根据需要把此窑洞窗口形状改造为矩形![]() ,其中E,F在边
,其中E,F在边![]() 上,G,H在圆弧
上,G,H在圆弧![]() 上.设
上.设![]() ,矩形
,矩形![]() 的面积为S.
的面积为S.
(1)求矩形![]() 的面积S关于变量
的面积S关于变量![]() 的函数关系式;
的函数关系式;
(2)求![]() 为何值时,矩形
为何值时,矩形![]() 的面积S最大?
的面积S最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:![]() x∈R,ax2﹣2ax+1>0,命题q:指数函数f(x)=ax(a>0且a≠1)为减函数,则P是q的( )
x∈R,ax2﹣2ax+1>0,命题q:指数函数f(x)=ax(a>0且a≠1)为减函数,则P是q的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com