
已知函数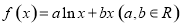 在点
在点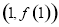 处的切线方程为
处的切线方程为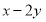
 .
.
(1)求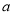 、
、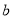 的值;
的值;
(2)当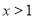 时,
时,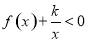 恒成立,求实数
恒成立,求实数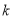 的取值范围;
的取值范围;
(3)证明:当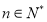 ,且
,且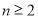 时,
时,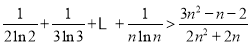 .
.
(1)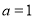 ,
,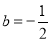 ;(2)
;(2)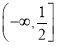 ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(1)利用已知条件得到两个条件:一是切线的斜率等于函数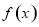 在
在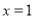 处的导数值
处的导数值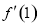 ,二是切点在切线上也在函数
,二是切点在切线上也在函数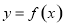 的图象上,通过切点
的图象上,通过切点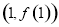 在切线上求出
在切线上求出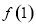 的值,然后再通过
的值,然后再通过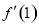 和
和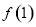 的值列有关
的值列有关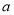 、
、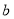 的二元一次方程组,求出
的二元一次方程组,求出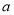 、
、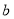 的值;(2)解法1是利用参数分离法将不等式
的值;(2)解法1是利用参数分离法将不等式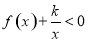 在区间
在区间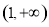 上恒成立问题转化为不等式
上恒成立问题转化为不等式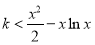 在区间
在区间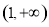 上恒成立,并构造函数
上恒成立,并构造函数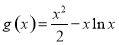 ,从而转化为
,从而转化为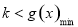 ,并利用导数求出函数
,并利用导数求出函数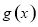 的最小值,从而求出
的最小值,从而求出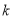 的取值范围;解法2是构造新函数
的取值范围;解法2是构造新函数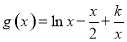 ,将不等式
,将不等式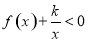 在区间
在区间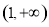 上恒成立问题转化为不等式
上恒成立问题转化为不等式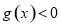 在区间
在区间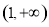 上恒成立问题,等价于
上恒成立问题,等价于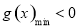 利用导数研究函数
利用导数研究函数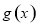 的单调性,对
的单调性,对 的取值进行分类讨论,通过在不同取值条件下确定函数
的取值进行分类讨论,通过在不同取值条件下确定函数 的单调性求出
的单调性求出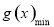 ,围绕
,围绕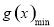
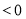 列不等式求解,从而求出
列不等式求解,从而求出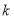 的取值范围;(3)在(2)的条件下得到
的取值范围;(3)在(2)的条件下得到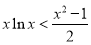 ,在不等式两边为正数的条件下两边取倒数得到
,在不等式两边为正数的条件下两边取倒数得到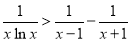 ,然后分别令
,然后分别令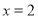 、
、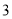 、
、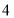 、
、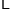 、
、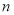 ,利用累加法以及同向不等式的相加性来证明问题中涉及的不等式.
,利用累加法以及同向不等式的相加性来证明问题中涉及的不等式.
试题解析:(1)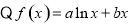 ,
,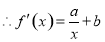 .
.
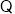 直线
直线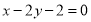 的斜率为
的斜率为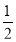 ,且过点
,且过点 ,
,
 ,即
,即 解得
解得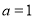 ,
,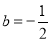 ;
;
(2)解法1:由(1)得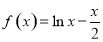 .
.
当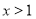 时,
时,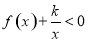 恒成立,即
恒成立,即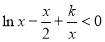 ,等价于
,等价于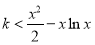 .
.
令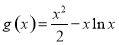 ,则
,则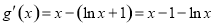 .
.
令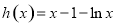 ,则
,则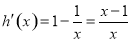 .
.
当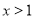 时,
时,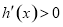 ,函数
,函数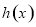 在
在 上单调递增,故
上单调递增,故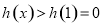 .
.
从而,当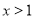 时,
时,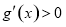 ,即函数
,即函数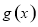 在
在 上单调递增,
上单调递增,
故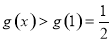 .
.
因此,当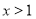 时,
时,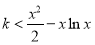 恒成立,则
恒成立,则 .
.
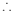 所求
所求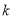 的取值范围是
的取值范围是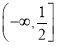 ;
;
解法2:由(1)得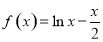 .
.
当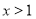 时,
时,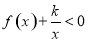 恒成立,即
恒成立,即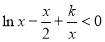 恒成立.
恒成立.
令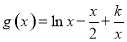 ,则
,则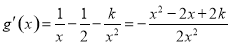 .
.
方程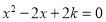 (*)的判别式
(*)的判别式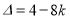 .
.
(ⅰ)当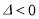 ,即
,即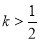 时,则
时,则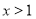 时,
时,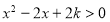 ,得
,得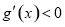 ,
,
故函数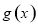 在
在 上单调递减.
上单调递减.
由于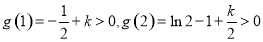 ,
,
则当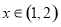 时,
时,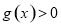 ,即
,即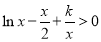 ,与题设矛盾;
,与题设矛盾;
(ⅱ)当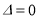 ,即
,即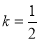 时,则
时,则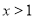 时,
时,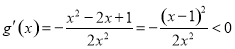 .
.
故函数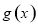 在
在 上单调递减,则
上单调递减,则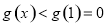 ,符合题意;
,符合题意;
(ⅲ)当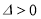 ,即
,即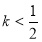 时,方程(*)的两根为
时,方程(*)的两根为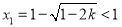 ,
,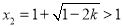 ,
,
则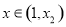 时,
时,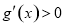 ,
,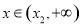 时,
时,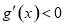 .
.
故函数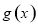 在
在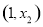 上单调递增,在
上单调递增,在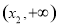 上单调递减,
上单调递减,
从而,函数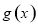 在
在 上的最大值为
上的最大值为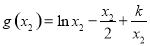 .
.
而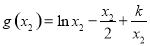
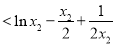 ,
,
由(ⅱ)知,当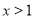 时,
时,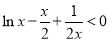 ,
,
得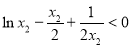 ,从而
,从而 .
.
故当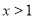 时,
时,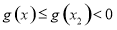 ,符合题意.
,符合题意.
综上所述,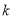 的取值范围是
的取值范围是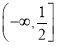 .
.
(3)由(2)得,当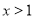 时,
时,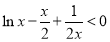 ,可化为
,可化为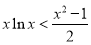 ,
,
又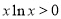 ,从而,
,从而,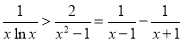 .
.
把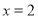 、
、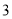 、
、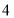 、
、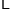 、
、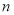 分别代入上面不等式,并相加得,
分别代入上面不等式,并相加得,
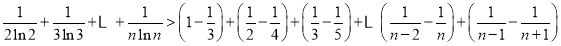
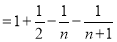
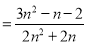 .
.
考点:1.导数的几何意义;2.不等式恒成立;3.参数分离法;4.分类讨论;5.数列不等式的证明


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源:2013-2014学年广东省揭阳市高三4月第二次模拟考试文科数学试卷(解析版) 题型:选择题
在平面直角坐标系中,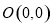 ,
,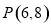 ,将向量
,将向量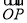 按逆时针旋转
按逆时针旋转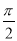 后,得向量
后,得向量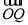 ,则点
,则点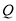 的坐标是( )
的坐标是( )
A.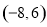 B.
B.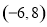 C.
C. D.
D.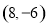
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省惠州市高三4月模拟考试文科数学试卷(解析版) 题型:选择题
如图,一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形,如果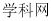 直角三角形的直角边长为
直角三角形的直角边长为 ,那么这个几何体的体积为 ( )
,那么这个几何体的体积为 ( )

A.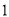 B.
B.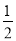 C.
C.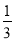 D.
D.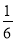
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com