
【题目】在直角坐标系xOy中,圆C1和C2的参数方程分别是 ![]() (φ为参数)和
(φ为参数)和 ![]() (φ为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(φ为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求圆C1和C2的极坐标方程;
(2)射线OM:θ=a与圆C1的交点为O、P,与圆C2的交点为O、Q,求|OP||OQ|的最大值.
【答案】
(1)解:圆C1 ![]() (φ为参数),
(φ为参数),
转化成直角坐标方程为:(x﹣2)2+y2=4
即:x2+y2﹣4x=0
转化成极坐标方程为:ρ2=4ρcosθ
即:ρ=4cosθ
圆C2 ![]() (φ为参数),
(φ为参数),
转化成直角坐标方程为:x2+(y﹣1)2=1
即:x2+y2﹣2y=0
转化成极坐标方程为:ρ2=2ρsinθ
即:ρ=2sinθ
(2)解:射线OM:θ=α与圆C1的交点为O、P,与圆C2的交点为O、Q
则:P(2+2cosα,2sinα),Q(cosα,1+sinα)
则:|OP|= ![]() =
= ![]() ,
,
|OQ|= ![]() =
= ![]()
则:|OP||OQ|= ![]()
= ![]()
设sinα+cosα=t( ![]() )
)
则: ![]()
则关系式转化为:
4 ![]() =
= ![]()
由于: ![]()
所以:(|OP||OQ|)max= ![]()
【解析】(1)首先把两圆的参数方程转化成直角坐标方程,再把直角坐标方程为转化成极坐标方程.(2)根据圆的坐标形式.利用两点间的距离公式,再利用换元法进一步求出最值.


科目:高中数学 来源: 题型:
【题目】如图,圆![]() 的半径为2,点
的半径为2,点![]() 是圆
是圆![]() 的六等分点中的五个点.
的六等分点中的五个点.

(1)从![]() 中随机取三点构成三角形,求这三点构成的三角形是直角三角形的概率;
中随机取三点构成三角形,求这三点构成的三角形是直角三角形的概率;
(2)在圆![]() 上随机取一点
上随机取一点![]() ,求
,求![]() 的面积大于
的面积大于![]() 的概率
的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
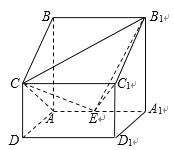
(Ⅰ)求四棱锥![]() 的体积;
的体积;
(Ⅱ)设点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长度;
的长度;
(Ⅲ)判断线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?(结论不要求证明)
?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某粮库拟建一个储粮仓如图所示,其下部是高为2的圆柱,上部是母线长为2的圆锥,现要设计其底面半径和上部圆锥的高,若设圆锥的高![]() 为
为![]() ,储粮仓的体积为
,储粮仓的体积为![]() .
.
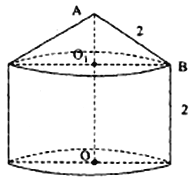
(1)求![]() 关于
关于![]() 的函数关系式;(圆周率用
的函数关系式;(圆周率用![]() 表示)
表示)
(2)求![]() 为何值时,储粮仓的体积最大.
为何值时,储粮仓的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:直线![]() ,一个圆与
,一个圆与![]() 轴正半轴与
轴正半轴与![]() 轴正半轴都相切,且圆心
轴正半轴都相切,且圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(![]() )求圆的方程.
)求圆的方程.
(![]() )
)![]() 是直线
是直线![]() 上的动点,
上的动点, ![]() ,
, ![]() 是圆的两条切线,
是圆的两条切线, ![]() ,
, ![]() 分别为切点,求四边形
分别为切点,求四边形![]() 的面积的最小值.
的面积的最小值.
(![]() )圆与
)圆与![]() 轴交点记作
轴交点记作![]() ,过
,过![]() 作一直线
作一直线![]() 与圆交于
与圆交于![]() ,
, ![]() 两点,
两点, ![]() 中点为
中点为![]() ,求
,求![]() 最大值.
最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com