
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,且直线
,且直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() .若直线
.若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,且
,且![]() 点为直线
点为直线![]() 上一点.
上一点.
(1)求![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 为椭圆
为椭圆![]() 的上顶点,直线
的上顶点,直线![]() 与
与![]() 轴交点
轴交点![]() ,记
,记![]() 表示面积,求
表示面积,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将曲线方程![]() ,先向左平移2个单位,再向上平移2个单位,得到曲线C.
,先向左平移2个单位,再向上平移2个单位,得到曲线C.
(1)点M(x,y)为曲线C上任意一点,写出曲线C的参数方程,并求出![]() 的最大值;
的最大值;
(2)设直线l的参数方程为![]() ,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a
(a![]() R),其中e为自然对数的底数.
R),其中e为自然对数的底数.
(1)若![]() ,求函数
,求函数![]() 的单调减区间;
的单调减区间;
(2)若函数![]() 的定义域为R,且
的定义域为R,且![]() ,求a的取值范围;
,求a的取值范围;
(3)证明:对任意![]() ,曲线
,曲线![]() 上有且仅有三个不同的点,在这三点处的切线经过坐标原点.
上有且仅有三个不同的点,在这三点处的切线经过坐标原点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 和函数
和函数![]() ,关于这两个函数图像的交点个数,下列四个结论:①当
,关于这两个函数图像的交点个数,下列四个结论:①当![]() 时,两个函数图像没有交点;②当
时,两个函数图像没有交点;②当![]() 时,两个函数图像恰有三个交点;③当
时,两个函数图像恰有三个交点;③当![]() 时,两个函数图像恰有两个交点;④当
时,两个函数图像恰有两个交点;④当![]() 时,两个函数图像恰有四个交点.正确结论的个数为( )
时,两个函数图像恰有四个交点.正确结论的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() 中,底面
中,底面![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() ,
,![]() 底面
底面![]() ,点
,点![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
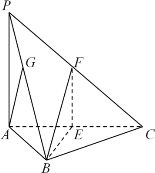
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角的余弦值为
所成的角的余弦值为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实现国家富强.民族复兴.人民幸福是“中国梦”的本质内涵.某商家计划以“全民健身促健康,同心共筑中国梦”为主题举办一次有奖消费活动,此商家先把某品牌乒乓球重新包装,包装时在每个乒乓球上印上“中”“国”“梦”三个字样中的一个,之后随机装盒(1盒4个球),并规定:若顾客购买的一盒球印的是同一个字,则此顾客获得一等奖;若顾客购买的一盒球集齐了“中”“国”二字且仅有此二字,则此顾客获得二等奖;若顾客购买的一盒球集齐了“中”“国”“梦”三个字,则此顾客获得三等奖,其它情况不设奖,则顾客购买一盒乒乓球获奖的概率是_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家政公司对部分员工的服务进行民意调查,调查按各项服务标准进行量化评分,婴幼儿保姆部对40~50岁和20~30岁各20名女保姆的调查结果如下:
分数 年龄 |
|
|
|
|
|
40~50岁 | 0 | 2 | 4 | 7 | 7 |
20~30岁 | 3 | 5 | 5 | 5 | 2 |
(1)若规定评分不低于80分为优秀保姆,试分别估计这两个年龄段保姆的优秀率;
(2)按照大于或等于80分为优秀保姆,80分以下为非优秀保姆统计.作出![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为对保姆工作质量的评价是否优秀与年龄有关.
的把握认为对保姆工作质量的评价是否优秀与年龄有关.
(3)从所有成绩在70分以上的人中按年龄利用分层抽样抽取10名保姆,再从这10人中选取3人给大家作经验报告,设抽到40~50岁的保姆的人数为![]() ,求出
,求出![]() 的分布列与期望值.
的分布列与期望值.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: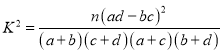 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com