
| π |
| 3 |
| π |
| 3 |
| 3 |
| 2 |
| π |
| 3 |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
| 3π |
| 4 |
| 3π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
| 2 |
| π |
| 3 |
| 3 |
| π |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 北师大课标高二版(选修2-2) 2009-2010学年 第39期 总第195期 北师大课标 题型:013
给出下列命题:
(1)若![]() >0,则f(x)>0;
>0,则f(x)>0;
(2)![]() dx=4;
dx=4;
(3)f(x)的原函数为F(x),且F(x)是以T为周期的函数,则![]() =
=![]() .
.
其中正确命题的个数为
1
2
3
0
查看答案和解析>>
科目:高中数学 来源: 题型:022
(
黄冈中学模拟)给出下列命题:A.若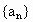 成等比数列,
成等比数列,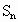 是前n项和,则
是前n项和,则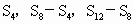 成等比数列;
成等比数列;
B.已知函数y=2sin(ωx+θ)为偶函数(0<θ<π),其图象与直线y=2的交点的横坐标为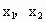 ,若
,若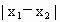 的最小值为π,则ω的值为2,θ的值为
的最小值为π,则ω的值为2,θ的值为 ;
;
C.函数y=f(x)的图象与直线x=a至多有一个交点;
D.函数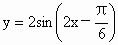 的图象的一个对称点是
的图象的一个对称点是 .
.
其中正确命题的代号是________(按照原顺序把你认为正确命题的代号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省仙桃市沔州中学高三(上)第二次月考数学试卷(文科)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com