
������11�֣���ͼ������ABCD�У�AB=6��BC=2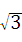 ����O��AB���е㣬��P��AB���ӳ���
����O��AB���е㣬��P��AB���ӳ��� �ϣ���BP=3��һ����E��O���������ÿ��1����λ���ȵ��ٶ���OA�����˶�������A���������ԭ�ٶ���AO���أ���һ����F��P��
�ϣ���BP=3��һ����E��O���������ÿ��1����λ���ȵ��ٶ���OA�����˶�������A���������ԭ�ٶ���AO���أ���һ����F��P�� ��������ÿ��1����λ���ȵ��ٶ�������PA�����˶�����E��Fͬʱ����������������ʱֹͣ�˶����ڵ�E��F���˶������У���EFΪ�����ȱߡ�EFG��ʹ��EFG�;���ABCD������PA��ͬ�࣮���˶���ʱ��Ϊt�루t��0����
��������ÿ��1����λ���ȵ��ٶ�������PA�����˶�����E��Fͬʱ����������������ʱֹͣ�˶����ڵ�E��F���˶������У���EFΪ�����ȱߡ�EFG��ʹ��EFG�;���ABCD������PA��ͬ�࣮���˶���ʱ��Ϊt�루t��0����
��1�����ȱߡ�EFG�ı�FGǡ�þ�����Cʱ�����˶�ʱ��t��ֵ��
��2���������˶������У���ȱߡ�EFG�;���ABCD�ص����ֵ���� ΪS�����S��t֮��ĺ�����ϵʽ����Ӧ���Ա���t��ȡֵ��Χ��
ΪS�����S��t֮��ĺ�����ϵʽ����Ӧ���Ա���t��ȡֵ��Χ��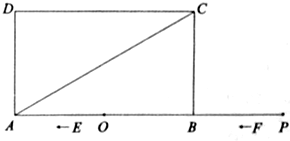
 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
����κ���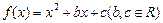 ,��֪����
,��֪����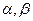 Ϊ��ʵ������
Ϊ��ʵ������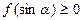 ,
,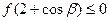
(1)��֤: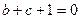 ��
��
( 2)��֤:
2)��֤: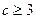 ��
��
(3)������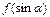 �����ֵΪ8,��
�����ֵΪ8,��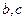 ֵ.
ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
����������14�֣�ij����˾ӵ������100��.��ÿ�����������Ϊ3000Ԫʱ����ȫ�����.��ÿ�����������ÿ����50Ԫʱ��δ����ij���������һ��.����ij�ÿ��ÿ����Ҫά����150Ԫ��δ����ij�ÿ��ÿ����Ҫ ά����50Ԫ.
ά����50Ԫ.
��1����ÿ�����������Ϊ3600Ԫʱ�����������������
��2����ÿ�����������Ϊ����Ԫʱ������˾���������������������Ƕ� �٣�
�٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
����С������12�֣���֪����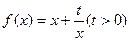 �͵�
�͵�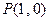 ������
������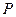 ������
������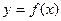 ����������
����������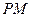 ��
��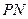 ���е�ֱ�Ϊ
���е�ֱ�Ϊ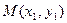 ��
��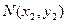 ��
��
��1����֤��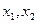 Ϊ����
Ϊ����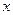 �ķ���
�ķ���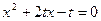 ��������
��������
��2����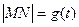 ������
������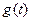 �ı���ʽ��
�ı���ʽ��
��3���ڣ�2���������£���������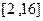 ���ܴ���
���ܴ���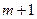 ��ʵ��
��ʵ��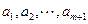 ��������ͬ����ʹ�ò���ʽ
��������ͬ����ʹ�ò���ʽ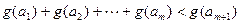 ��������
��������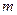 �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��14 �֣�ij����ÿ������ij�ֲ�Ʒ������40�������������������в�Ʒ����Ʒ��
�֣�ij����ÿ������ij�ֲ�Ʒ������40�������������������в�Ʒ����Ʒ��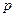 ��ÿ��������Ʒ����
��ÿ��������Ʒ���� (
(
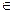
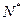 )��Ĺ�ϵΪ
)��Ĺ�ϵΪ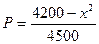 ��ÿ����һ����Ʒӯ��4000Ԫ��ÿ����һ����Ʒ����2000Ԫ.��ע����Ʒ��=��Ʒ����Ʒ�����²�Ʒ�ܼ�����100%��
��ÿ����һ����Ʒӯ��4000Ԫ��ÿ����һ����Ʒ����2000Ԫ.��ע����Ʒ��=��Ʒ����Ʒ�����²�Ʒ�ܼ�����100%��
����������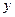 ��Ԫ����ʾ���ղ���
��Ԫ����ʾ���ղ��� �������ĺ�����
�����������
������ó����ղ���Ϊ���ټ�ʱ������������������������ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
����С������12�֣���֪ij��Ʒ�ļ۸�����x%�����۵������ͼ���mx%������mΪ���ij�����
��1����m=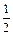 ʱ������Ʒ�ļ۸����Ƕ��٣�����ʹ���۵��ܽ�����
ʱ������Ʒ�ļ۸����Ƕ��٣�����ʹ���۵��ܽ�����
��2������ʵ����Ǽۣ���ʹ�����ܽ�����ӣ���m��ȡֵ��Χ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
����С������14�֣���֪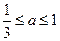 ��������
��������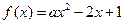 ������
������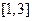 ��
��
�����ֵΪ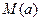 ����СֵΪ
����СֵΪ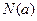 ����
����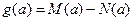 .
.
��1����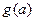 �ĺ�������ʽ��
�ĺ�������ʽ��
��2���жϺ���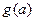 ������
������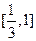 �ϵĵ����ԣ������
�ϵĵ����ԣ������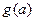 ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com