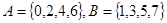练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设集合,从集合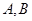中各取2个元素组成没有重复数字的四位数.
    （1）可组成多少个这样的四位数？
    （2）有多少个是2的倍数或是5的倍数？
    （1）756；（2）486.
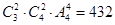    第一问中利用先选后排，第一类，不含0：有个，第二类，含0：有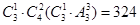个，然后由分类加法计数原理知，共有432+324=756个符合条件的数。
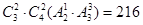    第二问中，利用因为是2的倍数即偶数，所以对于第一类，不含0：有个，第二类，含0：有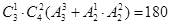个，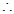
    共有216+180=396个；是5的倍数，只考虑末位数，即个位为5，同理有90个，解得。
    解：(1)先选后排
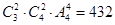    第一类，不含0：有个，第二类，含0：有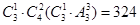个，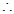
    由分类加法计数原理知，共有432+324=756个符合条件的数。   
    (2).是2的倍数即偶数，
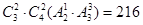    第一类，不含0：有个，第二类，含0：有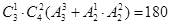个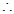， 共有216+180=396个
    是5的倍数，只考虑末位数，即个位为5，同理有90个，
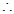    是2的倍数或者是5的倍数的无重复数字的四位数共有396+90=486个
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    5男生，2个女生排成一排，若女生不能排在两端但又必须相邻，则不同的排法有（     ）
    A．480B．960C．720D．1440

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    25人排成5×5方阵,现从中选3人,要求3人不在同一行也不在同一列,不同的选法有      种.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    从4名男生,3名女生中选出三名代表。
    (1)不同的选法共有多少种?
    (2)至少有一名女生的不同的选法共有多少种?
    (3)代表中男、女生都要有的不同的选法共有多少种?

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    篮球队从甲、乙等名队员中挑选名上场比赛，要求甲、乙中至少有人参加，则下列选派方法种数表示不正确的是（ ▲ ）
    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    给定数字0、1、2、3、5、9每个数字最多用一次
    （1）可能组成多少个四位数？
    （2）可能组成多少个四位奇数？
    （3）可能组成多少个自然数？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    将一四棱锥(图6)的每个顶点染一种颜色，并使同一条棱的两端点异色，若只有五种颜色可供使用，则不同的染色方法共            种
     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    若，则      ▲    ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    ＝　　　　　．

    查看答案和解析>>

    同步练习册答案