
分析 依题意F(c,0),其中c2=a2-b2,通过设直线BM的方程:y=$2\sqrt{6}$(x-c)可知M(0,-$2\sqrt{6}$c),通过设B(p,q)可知q=$2\sqrt{6}$(p-c),利用B分$\overrightarrow{MF}$所成的比为2可知$\overrightarrow{MB}$=2$\overrightarrow{BF}$,从而(p-0,q+$2\sqrt{6}$c)=2(c-p,0-q),计算可知p=$\frac{2}{3}$c、q=-$\frac{2\sqrt{6}}{3}$c,将其代入$\frac{{p}^{2}}{{a}^{2}}$+$\frac{{q}^{2}}{{b}^{2}}$=1、化简可知24•$\frac{{a}^{2}}{{b}^{2}}$-4•$\frac{{b}^{2}}{{a}^{2}}$=29,利用换元法、计算可知$\frac{{a}^{2}}{{b}^{2}}$=$\frac{4}{3}$,从而$\frac{{b}^{2}}{{a}^{2}}$=$\frac{3}{4}$,利用e2=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}$计算即得结论.
解答  解:如图,F(c,0),其中c2=a2-b2,
解:如图,F(c,0),其中c2=a2-b2,
设直线BM的方程为:y=$2\sqrt{6}$(x-c),则M(0,-$2\sqrt{6}$c),
设B(p,q),则q=$2\sqrt{6}$(p-c)、$\frac{{p}^{2}}{{a}^{2}}$+$\frac{{q}^{2}}{{b}^{2}}$=1,
∵B分$\overrightarrow{MF}$所成的比为2,
∴$\overrightarrow{MB}$=2$\overrightarrow{BF}$,即(p-0,q+$2\sqrt{6}$c)=2(c-p,0-q),
∴p=2c-2p、q+$2\sqrt{6}$c=-2q,即p=$\frac{2}{3}$c、q=-$\frac{2\sqrt{6}}{3}$c,
又∵$\frac{{p}^{2}}{{a}^{2}}$+$\frac{{q}^{2}}{{b}^{2}}$=1,即$\frac{(\frac{2}{3}c)^{2}}{{a}^{2}}$+$\frac{(-\frac{2\sqrt{6}}{3}c)^{2}}{{b}^{2}}$=1,
∴$\frac{4({a}^{2}-{b}^{2})}{9{a}^{2}}$+$\frac{24({a}^{2}-{b}^{2})}{9{b}^{2}}$=1,
化简得:24•$\frac{{a}^{2}}{{b}^{2}}$-4•$\frac{{b}^{2}}{{a}^{2}}$=29,
令t=$\frac{{a}^{2}}{{b}^{2}}$,则上式可化为:24t-$\frac{4}{t}$=29,
∴24t2-29t-4=0,
解得:t=$\frac{29±\sqrt{29×29+4×24×4}}{2×24}$=$\frac{29±35}{48}$,
∴t=$\frac{4}{3}$或t=-$\frac{1}{8}$(舍),
即$\frac{{a}^{2}}{{b}^{2}}$=$\frac{4}{3}$,∴$\frac{{b}^{2}}{{a}^{2}}$=$\frac{3}{4}$,
∴e2=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}$=1-$\frac{{b}^{2}}{{a}^{2}}$=1-$\frac{3}{4}$=$\frac{1}{4}$,
∴椭圆的离心率e=$\frac{1}{2}$.
点评 本题考查椭圆的离心率,涉及向量、勾股定理等基础知识,注意解题方法的积累,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 如图,空间四边形ABCD各边边长均为a,M,N分别是对角线BD,AC的中点.
如图,空间四边形ABCD各边边长均为a,M,N分别是对角线BD,AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
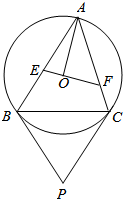 如图,锐角△ABC内接于圆0.过圆心0且垂直于半径0A的直线分别交边AB、AC于点E、F.设圆0在B、C两点处的切线相交于点P.求证:直线AP平分线段EF.
如图,锐角△ABC内接于圆0.过圆心0且垂直于半径0A的直线分别交边AB、AC于点E、F.设圆0在B、C两点处的切线相交于点P.求证:直线AP平分线段EF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 装潢师小王在墙面上设计了如图所示的一个图案,已知四边形四个顶点都在圆周上,且AD=DC=4m,BC=6m,∠A=120°,现在小王想买乳胶漆给四边形ABCD涂色,依据设计方案四边形的四边涂成红色,四边形内部要涂成蓝色,他想根据线段的长度与四边形的面积来买乳胶漆.请你帮他计算:
装潢师小王在墙面上设计了如图所示的一个图案,已知四边形四个顶点都在圆周上,且AD=DC=4m,BC=6m,∠A=120°,现在小王想买乳胶漆给四边形ABCD涂色,依据设计方案四边形的四边涂成红色,四边形内部要涂成蓝色,他想根据线段的长度与四边形的面积来买乳胶漆.请你帮他计算:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com