Question

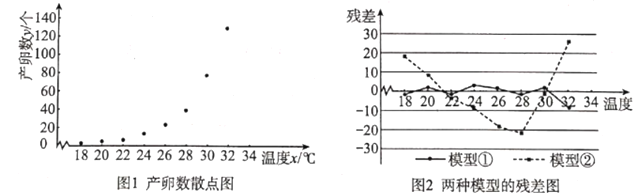
【题目】红铃虫（Pectinophora gossypiella）是棉花的主要害虫之一，其产卵数与温度有关.现收集到一只红铃虫的产卵数y（个）和温度x（℃）的8组观测数据，制成图1所示的散点图.现用两种模型①，②分别进行拟合，由此得到相应的回归方程并进行残差分析，进一步得到图2所示的残差图.

根据收集到的数据，计算得到如下值：

25	2.89	646	168	422688	48.48	70308

表中；；；；

（1）根据残差图，比较模型①、②的拟合效果，应选择哪个模型？并说明理由；

（2）根据（1）中所选择的模型，求出y关于x的回归方程（系数精确到0.01），并求温度为34℃时，产卵数y的预报值.

（参考数据：，，，）

附：对于一组数据，，…，，其回归直线的斜率和截距的最小二乘估计分别为，.

Answer 1

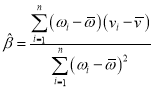【答案】（1）应该选择模型①.见解析（2）；250个

【解析】

（1）由模型①的残差点比较均匀落在水平的带状区域以及带状区域的宽度窄，所以选择模型①比较合适；

（2）令，z与温度x可以用线性回归方程来拟合，则，利用公式和数据求出和，则可以得到y关于温度x的回归方程，当时，可求出产卵数y的预报值.

（1）应该选择模型①.

由于模型①残差点比较均匀地落在水平的带状区域中，

且带状区域的宽度比模型②带状宽度窄，所以模型①的拟合精度更高，

回归方程的预报精度相应就会越高，故选模型①比较合适

（2）令，z与温度x可以用线性回归方程来拟合，则.

，

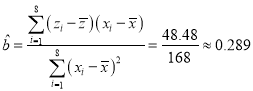所以，

则z关于x的线性回归方程为.

于是有，

所以产卵数y关于温度x的回归方程为

当时，（个）.

所以，在气温在34℃时，一个红铃虫的产卵数的预报值为250个