
设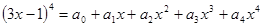 。
。
求:(1)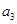
(2)求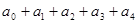 ;
;
(3)求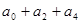 ;
;
(4)求各项二项式系数的和.
(1) -108 (2)16 (3)136 (4)16
【点评】①要注意二项展开式各项的系数与二项式系数是不同的两个概念;②系数和与二项式系数和不一定相同,本题的(2)与(4)结果相同纯属巧合;③注意求系数和上述是最一般的方法,一定要理解.
【解析】可把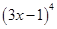 按照二项式定理展开
即
按照二项式定理展开
即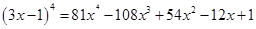 ,(1)、(2)、(3)都可解决。也可以赋值求解;二项式系数是
,(1)、(2)、(3)都可解决。也可以赋值求解;二项式系数是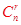 ,把
,把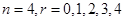
分别代入求和得
(1) -108 ……3分
(2)令x=1得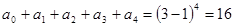 ;……6分
;……6分
(3)令x=-1得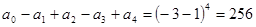 ,
,
而由(2)知: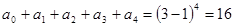 ,
,
两式相加得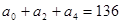 ;……10分
;……10分
(4)各项二项式系数的和为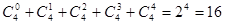 .……14分
.……14分
点评:①要注意二项展开式各项的系数与二项式系数是不同的两个概念;②系数和与二项式系数和不一定相同,本题的(2)与(4)结果相同纯属巧合;③注意求系数和上述是最一般的方法,一定要理解


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2011-2012学年江苏省苏北四市高三第三次模拟考试数学试卷(解析版) 题型:解答题
(本小题满分16分)
数列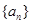 的前n项和为
的前n项和为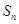 ,存在常数A,B,C,使得
,存在常数A,B,C,使得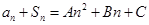 对任意正整数n都成立。
对任意正整数n都成立。
(1) 若数列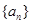 为等差数列,求证:3A-B+C=0;
为等差数列,求证:3A-B+C=0;
(2) 若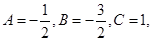 设
设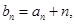 数列
数列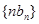 的前n项和为
的前n项和为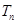 ,求
,求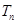 ;
;
(3) 若C=0,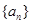 是首项为1的等差数列,设
是首项为1的等差数列,设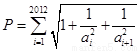 ,求不超过P的最大整数的值。
,求不超过P的最大整数的值。
查看答案和解析>>
科目:高中数学 来源:2013届广东省高二第七学段考试理科数学试卷(解析版) 题型:解答题
(本小题14分)请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱(底面是正方形的直棱柱)形状的包装盒,E、F在AB上是被切去的等腰直角三角形HEF斜边的两个端点,设AE=FB=xcm.

(1)请用 分别表示|GE|、|EH|的长
分别表示|GE|、|EH|的长
(2)若广告商要求包装盒侧面积S(cm2)最大,试问x应取何值?
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com