
【题目】以下给出五个命题,其中真命题的序号为______
①函数![]() 在区间
在区间![]() 上存在一个零点,则
上存在一个零点,则![]() 的取值范围是
的取值范围是![]() 或
或![]() ;
;
②“任意菱形的对角线一定相等”的否定是“菱形的对角线一定不相等”;
③![]() ,
,![]() ;
;
④若![]() ,则
,则![]() ;
;
⑤“![]() ”是“
”是“![]() 成等比数列”的充分不必要条件.
成等比数列”的充分不必要条件.
科目:高中数学 来源: 题型:
【题目】某企业为打入国际市场,决定从![]() 两种产品中只选择一种进行投资生产.已知投资生产这两种产品的有关数据如下表:(单位:万美元)
两种产品中只选择一种进行投资生产.已知投资生产这两种产品的有关数据如下表:(单位:万美元)

其中年固定成本与年生产的件数无关,![]() 为待定常数,其值由生产
为待定常数,其值由生产![]() 产品的原材料价格决定,预计
产品的原材料价格决定,预计![]() .另外,年销售
.另外,年销售![]() 件
件![]() 产品时需上交
产品时需上交![]() 万美元的特别关税.假设生产出来的产品都能在当年销售出去.
万美元的特别关税.假设生产出来的产品都能在当年销售出去.
(1)写出该厂分别投资生产![]() 两种产品的年利润
两种产品的年利润![]() 与生产相应产品的件数
与生产相应产品的件数![]() 之间的函数关系,并指明其定义域;
之间的函数关系,并指明其定义域;
(2)如何投资才可获得最大年利润?请你做出规划.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设H1(x)=max![]() ,H2(x)=min
,H2(x)=min![]() (max
(max![]() 表示p,q中的较大值,min
表示p,q中的较大值,min![]() 表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
A.16B.-16
C.a2-2a-16D.a2+2a-16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)=(a-x)|x|,常数a∈R,且关于x的不等式mx2+m>f[f(x)]对所有的x∈[-2,2]恒成立,则实数m的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() 。
。
(1)若点![]() 在圆
在圆![]() 内,求
内,求![]() 的取值范围;
的取值范围;
(2)若过点![]() 的圆
的圆![]() 的切线只有一条,求切线的方程;
的切线只有一条,求切线的方程;
(3)当![]() 时,过点
时,过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程。
的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为![]() 、
、![]() 、
、![]() 三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
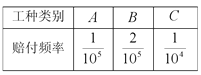

(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
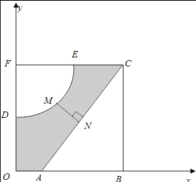
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,河的两岸分别有生活小区![]() 和
和![]() ,其中
,其中![]() ,
,![]() 三点共线,
三点共线,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,测得
,测得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,若以
,若以![]() 所在直线分别为
所在直线分别为![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() 则河岸
则河岸![]() 可看成是曲线
可看成是曲线![]() (其中
(其中![]() 是常数)的一部分,河岸
是常数)的一部分,河岸![]() 可看成是直线
可看成是直线![]() (其中
(其中![]() 为常数)的一部分.
为常数)的一部分.
(1)求![]() 的值.
的值.
(2)现准备建一座桥![]() ,其中
,其中![]() 分别在
分别在![]() 上,且
上,且![]() ,
,![]() 的横坐标为
的横坐标为![]() .写出桥
.写出桥![]() 的长
的长![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ,并标明定义域;当
,并标明定义域;当![]() 为何值时,
为何值时,![]() 取到最小值?最小值是多少?
取到最小值?最小值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com