
【题目】已知函数f(x)=﹣x3+ax2+bx+c图象上的点P(1,﹣2)处的切线方程为y=﹣3x+1.
(1)若函数f(x)在x=﹣2时有极值,求f(x)的表达式
(2)若函数f(x)在区间[﹣2,0]上单调递增,求实数b的取值范围.
【答案】
(1)解:f′(x)=﹣3x2+2ax+b,
因为函数f(x)在x=1处的切线斜率为﹣3,
所以f′(1)=﹣3+2a+b=﹣3,即2a+b=0,
又f(1)=﹣1+a+b+c=﹣2得a+b+c=﹣1.
函数f(x)在x=﹣2时有极值,所以f'(﹣2)=﹣12﹣4a+b=0,
解得a=﹣2,b=4,c=﹣3,
所以f(x)=﹣x3﹣2x2+4x﹣3
(2)解:因为函数f(x)在区间[﹣2,0]上单调递增,所以导函数f′(x)=﹣3x2﹣bx+b
在区间[﹣2,0]上的值恒大于或等于零,
则 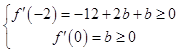 得b≥4,所以实数b的取值范围为[4,+∞).
得b≥4,所以实数b的取值范围为[4,+∞).
【解析】(1)对函数f(x)求导,由题意点P(1,﹣2)处的切线方程为y=﹣3x+1,可得f′(1)=﹣3,再根据f(1)=﹣1,又由f′(﹣2)=0联立方程求出a,b,c,从而求出f(x)的表达式.(2)由题意函数f(x)在区间[﹣2,0]上单调递增,对其求导可得f′(x)在区间[﹣2,0]大于或等于0,从而求出b的范围.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】若(2-![]() x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5.求:
x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5.求:
(1)|a0|+|a1|+|a2|+|a3|+|a4|+|a5|;
(2)(a0+a2+a4)2-(a1+a2+a3)2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系中椭圆C的方程为ρ2= ![]() ,以极点为原点,极轴为x轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
,以极点为原点,极轴为x轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
(1)求该椭圆的直角标方程,若椭圆上任一点坐标为P(x,y),求x+ ![]() y的取值范围;
y的取值范围;
(2)若椭圆的两条弦AB,CD交于点Q,且直线AB与CD的倾斜角互补,求证:|QA||QB|=|QC||QD|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,江的两岸可近似的看成两平行的直线,江岸的一侧有A,B两个蔬菜基地,江的另一侧点C处有一个超市.已知A、B、C中任意两点间的距离为20千米.超市欲在AB之间建一个运输中转站D,A,B两处的蔬菜运抵D处后,再统一经过货轮运抵C处.由于A,B两处蔬菜的差异,这两处的运输费用也不同.如果从A处出发的运输费为每千米2元,从B处出发的运输费为每千米1元,货轮的运输费为每千米3元. 
(1)设∠ADC=α,试将运输总费用S(单位:元)表示为α的函数S(α),并写出自变量的取值范围;
(2)问中转站D建在何处时,运输总费用S最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若函数![]() 在区间
在区间![]() 上是单调递增函数,求实数
上是单调递增函数,求实数![]() 的最大值;
的最大值;
(Ⅲ)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有两个实数根
内有两个实数根![]() ,分别求实数
,分别求实数![]() 与
与![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com