
����Ŀ��ijͶ�ʹ�˾�ƻ�Ͷ��A��B���ֽ��ڲ�Ʒ�������г�������Ԥ�⣬A��Ʒ������y1��Ͷ�ʽ��x�ĺ�����ϵΪy1=18�� ![]() ��B��Ʒ������y2��Ͷ�ʽ��x�ĺ�����ϵΪy2=
��B��Ʒ������y2��Ͷ�ʽ��x�ĺ�����ϵΪy2= ![]() ��ע��������Ͷ�ʽ�λ����Ԫ����
��ע��������Ͷ�ʽ�λ����Ԫ����
��1���ù�˾����100��Ԫ�ʽ𣬲�ȫ��Ͷ��A��B���ֲ�Ʒ�У�����x��Ԫ�ʽ�Ͷ��A��Ʒ����A��B���ֲ�Ʒ�����ܺͱ�ʾΪx�ĺ�������д��������
��2���ڣ�1���������£����ʣ�����������100��Ԫ�ʽ𣬲���ʹ��˾�������������������Ϊ������Ԫ��
���𰸡�
��1���⣺����x��Ԫ�ʽ�Ͷ��A��Ʒ����ʣ���100��x����Ԫ���ʽ�Ͷ��B��Ʒ��
�����ܺ�f��x��=18�� ![]() +
+ ![]() =38��
=38�� ![]() ��
�� ![]() ��x��[0��100]����
��x��[0��100]����
��2���⣺��f��x��=40�� ![]() ��
�� ![]() ��x��[0��100]��
��x��[0��100]��
���ɻ�������ʽ�ã�f��x����40��2 ![]() =28��ȡ�Ⱥţ����ҽ���
=28��ȡ�Ⱥţ����ҽ��� ![]() =
= ![]() ʱ����x=20���𣺷ֱ���20��Ԫ��80��Ԫ�ʽ�Ͷ��A��B���ֽ��ڲ�Ʒ������ʹ��˾�����������������Ϊ28��Ԫ��
ʱ����x=20���𣺷ֱ���20��Ԫ��80��Ԫ�ʽ�Ͷ��A��B���ֽ��ڲ�Ʒ������ʹ��˾�����������������Ϊ28��Ԫ��
����������1������x��Ԫ�ʽ�Ͷ��A��Ʒ����ʣ���100��x����Ԫ���ʽ�Ͷ��B��Ʒ������A��Ʒ������y1��Ͷ�ʽ��x�ĺ�����ϵΪy1=18�� ![]() ��B��Ʒ������y2��Ͷ�ʽ��x�ĺ�����ϵΪy2=
��B��Ʒ������y2��Ͷ�ʽ��x�ĺ�����ϵΪy2= ![]() ���ɵ������ܺͣ���2��f��x��=40��
���ɵ������ܺͣ���2��f��x��=40�� ![]() ��
�� ![]() ��x��[0��100]���ɻ�������ʽ���ɵý��ۣ�
��x��[0��100]���ɻ�������ʽ���ɵý��ۣ�


 ��ĩ100�ִ��غ�������ϵ�д�
��ĩ100�ִ��غ�������ϵ�д� Сѧ�������Ծ�ϵ�д�
Сѧ�������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ȡij��ѧ���������10��ͬѧ���������ǵ����ߣ���λ��cm��������������ݵľ�Ҷͼ��ͼ�� 
��1�����ݾ�Ҷͼ�ж��ĸ����ƽ�����߽ϸߣ�
��2������װ���������
��3���ִ��Ұ���10��ͬѧ�������ȡ�������߲�����173cm��ͬѧ��������Ϊ176cm��ͬѧ�����еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ�洹ֱ���������⣺ ��һ��ƽ���ڵ���ֱ֪�߱ش�ֱ����һ��ƽ���ڵ�����һ��ֱ�ߣ�
��һ��ƽ���ڵ���ֱ֪�߱ش�ֱ����һ��ƽ���ڵ�������ֱ�ߣ�
��һ��ƽ���ڵ���һ��ֱ�߱ش�ֱ����һ��ƽ�森
��һ��ƽ���ڴ�ֱ�ڽ��ߵ�ֱ������һ��ƽ�洹ֱ��
������ȷ����ĸ����ǣ� ��
A.3
B.2
C.1
D.0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ʽ��  ��ʾ��ƽ������ΪD����
��ʾ��ƽ������ΪD����
��1��z=x2+y2����СֵΪ ��
��2��������y=|2x��1|+m��ͼ���ϴ�������D�ϵĵ㣬��ʵ��m��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}�У�a1=1����ǰn���ΪSn �� ������an= ![]() ��n��2��
��n��2��
��1����Sn��
��2��֤������n��2ʱ��S1+ ![]() S2+
S2+ ![]() S3+��+
S3+��+ ![]() Sn��
Sn�� ![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ij����ѧ�������������������ѧ���Գɼ��ľ�Ҷͼ����1�ε��ڵ�14�εĿ��Գɼ����μ�ΪA1 �� A2 �� ��A14 �� ��ͼ2��ͳ�ƾ�Ҷͼ�гɼ���һ����Χ�ڿ��Դ�����һ���㷨����ͼ����ô�㷨����ͼ����Ľ���ǣ� �� 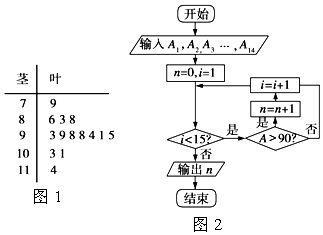
A.7
B.8
C.9
D.10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʵ��a��b����a+b=1���� ��
A.![]() �����ֵ4
�����ֵ4
B.ab����Сֵ ![]()
C.![]() �����ֵ
�����ֵ ![]()
D.a2+b2����Сֵ ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ƽ������ ![]() =��x��y������
=��x��y������ ![]() �����������ʱ�뷽����ת�Ƚǵõ�������
�����������ʱ�뷽����ת�Ƚǵõ������� ![]() =��xcos�ȩ�ysin�ȣ�xsin��+ycos�ȣ��������ѵ�B�Ƶ�A��ʱ�뷽����ת�ȵõ���P��
=��xcos�ȩ�ysin�ȣ�xsin��+ycos�ȣ��������ѵ�B�Ƶ�A��ʱ�뷽����ת�ȵõ���P��
��1����֪ƽ���ڵ�A��2��3������B��2+2 ![]() ��1�����ѵ�B�Ƶ�A��ʱ�뷽����ת
��1�����ѵ�B�Ƶ�A��ʱ�뷽����ת ![]() �ǵõ���P�����P�����꣮
�ǵõ���P�����P�����꣮
��2����ƽ��������C�ϵ�ÿһ��������ԭ����˳ʱ�뷽����ת ![]() ��õ��ĵ�Ĺ켣����������y=
��õ��ĵ�Ĺ켣����������y= ![]() ����ԭ������C�ķ��̣�
����ԭ������C�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=log4��4x+1��+2kx��k��R����ż������
��1����k��ֵ��
��2��������f��x��=m�н⣬��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com