
 和P(P>0)假设每轮训练中两组都各有两项训练任务需完成,并且每项任务的完成与否互不影响.若在一轮冬训中,两组完成训练任务的项数相等且都不小于一项,则称甲、乙两组为“友好组”
和P(P>0)假设每轮训练中两组都各有两项训练任务需完成,并且每项任务的完成与否互不影响.若在一轮冬训中,两组完成训练任务的项数相等且都不小于一项,则称甲、乙两组为“友好组” 求甲、乙两组在完成一轮冬训中成为“友好组”的概率;
求甲、乙两组在完成一轮冬训中成为“友好组”的概率; ,当
,当 时,求P的取值范围.
时,求P的取值范围.科目:高中数学 来源:不详 题型:解答题
| | 轿车A | 轿车B | 轿车C |
| 舒适型 | 100 | 150 | Z |
| 标准型 | 300 | 450 | 600 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 排队人数 |  |  |  |  |  |  人以上 人以上 |
| 概率 |  |  |  |  |  |  |
 人排队的概率是多少?
人排队的概率是多少?  人排队的概率是多少
人排队的概率是多少查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的高二(1)班男同学有
的高二(1)班男同学有 名,女同学有
名,女同学有 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个 人的课外兴趣小组.
人的课外兴趣小组. 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;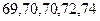 ,第二次做试验的乙同学得
,第二次做试验的乙同学得 到的试验数据为
到的试验数据为 ,请问哪位同学的实验更稳定?并说明理由.
,请问哪位同学的实验更稳定?并说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 拐入同一公路时,需要有一车等待.已知甲车拐入需要的时间为2分钟,乙车拐入需要的时间为1分钟,倘若甲、乙两车都在某5分
拐入同一公路时,需要有一车等待.已知甲车拐入需要的时间为2分钟,乙车拐入需要的时间为1分钟,倘若甲、乙两车都在某5分 钟内到达转弯路口,则至少有一辆车转弯时需要
钟内到达转弯路口,则至少有一辆车转弯时需要 等待的概率
等待的概率 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com