
【题目】设 ![]() ,对任意x∈R,不等式a(cos2x﹣m)+πcosx≥0恒成立,则实数m的取值范围为 .
,对任意x∈R,不等式a(cos2x﹣m)+πcosx≥0恒成立,则实数m的取值范围为 .
【答案】(﹣∞,﹣3]
【解析】解:∵ ![]() ,表示y=
,表示y= ![]() 在[0,1]上的积分,也得圆面积的四分之一, ∴a=
在[0,1]上的积分,也得圆面积的四分之一, ∴a= ![]() ×π,
×π,
∴对任意x∈R,不等式 ![]() (cos2x﹣m)+πcosx≥0恒成立,
(cos2x﹣m)+πcosx≥0恒成立,
可得m≤cos2x+4cosx在x∈R上恒成立,cosx∈[﹣1,1],
求出cos2x+4cosx的最小值即可,cos2x+4cosx=(cosx+2)2﹣4,
∵函数开口向上,cosx∈[﹣1,1],
函数f(cosx)=cos2x+4cosx在[﹣1,1]上增函数,当cosx=﹣1时取得最小值,可得(﹣1)2+4×(﹣1)=﹣3,
∴cos2x+4cosx的最小值为﹣3,
∴m≤﹣3,
所以答案是(﹣∞,﹣3];
【考点精析】利用定积分的概念对题目进行判断即可得到答案,需要熟知定积分的值是一个常数,可正、可负、可为零;用定义求定积分的四个基本步骤:①分割;②近似代替;③求和;④取极限.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}中各项都大于1,前n项和为Sn , 且满足an2+3an=6Sn﹣2.
(1)求数列{an}的通项公式;
(2)令bn= ![]() ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;
(3)求使得Tn< ![]() 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省的一个气象站观测点在连续4天里记录的![]() 指数
指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位:
(单位: ![]() )的情况如表1:
)的情况如表1:

该省某市2016年11月![]() 指数频数分布如表2:
指数频数分布如表2:
|
|
|
|
|
|
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(附参考公式: ![]() ,其中
,其中 ,
, ![]() )
)
(2)小李在该市开了一家洗车店,经统计,洗车店平均每天的收入与![]() 指数由相关关系,如表3:
指数由相关关系,如表3:
|
|
|
|
|
|
日均收入(元) |
|
|
|
|
|
根据表3估计小李的洗车店该月份平均每天的收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a≥0,f(x)=x﹣1﹣ln2x+2alnx(x>0). (Ⅰ)令F(x)=xf′(x),讨论F(x)在(0,+∞)内的单调性并求极值;
(Ⅱ)求证:当x>1时,恒有x>ln2x﹣2alnx+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对某渔业产品的质量调研中,从甲、乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).如图是测量数据的茎叶图: 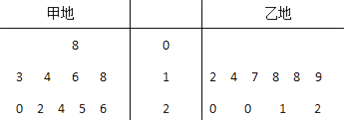
规定:当产品中的此种元素含量≥15毫克时为优质品.
(Ⅰ)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数);
(Ⅱ)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数ξ的分布列及数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列不等式:①x≥ln(x+1)(x>﹣1)② ![]() >﹣
>﹣ ![]() +2x﹣
+2x﹣ ![]() (x>0)③ln
(x>0)③ln ![]() >2(x+
>2(x+ ![]() )(x∈(0,1))其中成立的个数是( )
)(x∈(0,1))其中成立的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com