
【题目】某市居民自来水收费标准如下:每户每月用水量不超过4吨时,每吨为2元;当用水量超4吨时,超过部分每吨为3元.八月甲、乙两用户共交水费![]() 元,已知甲、乙两用户月用水量分别为
元,已知甲、乙两用户月用水量分别为![]() 吨、
吨、![]() 吨.
吨.
(1)求![]() 关于
关于![]() 的函数;
的函数;
(2)若甲、乙两用户八月共交34元,分别求甲、乙两用户八月的用水量和水费.
【答案】(1)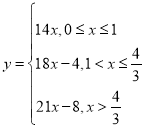
(2)甲、乙两用户八月的用水量分别为![]() ,
,![]() ,水费分别为20元、14元
,水费分别为20元、14元
【解析】
(1)对甲、乙两用户用水情况分3种情况考虑,甲不超过4吨;甲超过4吨、乙不超过4吨;甲超过4吨、乙也超过4吨;从得到![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)由(1)得到的分段函数,讨论各段函数值为34时,从而求得![]() ,再进一步求得甲、乙各自的用水量和水费.
,再进一步求得甲、乙各自的用水量和水费.
(1)由题意得:
①甲不超过4吨,则乙也必定不超过4吨,
所以![]() ,即
,即![]() 时,
时,![]() ;
;
②甲超过4吨、乙不超过4吨,
所以![]() 时,
时,![]() ;
;
③甲超过4吨、乙也超过4吨,
所以![]()
![]() 时,
时,![]() .
.
综上所述: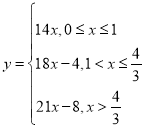 .
.
(2)当![]() 时,
时,![]() (舍);
(舍);
当![]() 时,
时,![]() (舍),
(舍),
![]() .
.
当![]() 时,
时,![]() ,
,
甲、乙用水分别![]() ,
,![]() ,
,
设甲、乙的水费分别![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() 甲、乙两用户八月的用水量分别为
甲、乙两用户八月的用水量分别为![]() ,
,![]() ,水费分别为20元、14元.
,水费分别为20元、14元.


科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民收入逐年增长.某地区2014年至2018年农村居民家庭人均纯收入![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
人均纯收入 | 5 | 4 | 7 | 8 | 10 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2014年至2018年该地区农村居民家庭人均纯收入的变化情况,并预测2019年该地区农村居民家庭人均纯收入为多少?
附:回归直线的斜率和截距的最小二乘估计公式分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用适当的方法表示下列集合:
(1)方程组![]() 的解集;
的解集;
(2)方程![]() 的实数根组成的集合;
的实数根组成的集合;
(3)平面直角坐标系内所有第二象限的点组成的集合;
(4)二次函数![]() 的图象上所有的点组成的集合;
的图象上所有的点组成的集合;
(5)二次函数![]() 的图象上所有点的纵坐标组成的集合.
的图象上所有点的纵坐标组成的集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com