
分析 (1)利用函数的奇偶性列出方程组,转化求解函数的解析式即可.
(2)求出两个命题为真命题时,a的范围,然后利用复合命题求解即可.
解答 解:(1)∵f(x)+g(x)=a2x3+x2+a3①,
f(x)为奇函数,g(x)为偶函数,
-f(x)+g(x)=-a2x3+x2+a3②,
解得f(x)=a2x3,g(x)=x2+a3 a≠0,a∈R.
(2)若p真,f(x)min≥1,x∈[1,2],
∴a2≥1?a≥1或a≤-1,
若q真,g(x)min≥17,
即9+a3≥17解得a≥2,
P∨Q为真,
则a的范围为:(-∞,-1]∪[1,+∞].
点评 本题考查命题的真假的判断,函数的奇偶性的应用,函数的解析式的求法,考查计算能力.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | a<b<c | C. | a<c<b | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
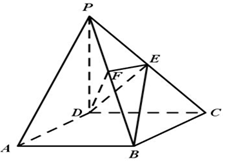 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC中点,作EF⊥PB,交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC中点,作EF⊥PB,交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1<x3<x2 | B. | x2<x1<x3 | C. | x1<x2<x3 | D. | x3<x1<x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 必要而不充分条件 | ||
| C. | 充分而不必要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com