
 x2+(a-3)x+1恒成立,试求实数a的取值范围.
x2+(a-3)x+1恒成立,试求实数a的取值范围. x2+(a-3)x+1得
x2+(a-3)x+1得 x2+(a-3)x+1即ax≤ex-
x2+(a-3)x+1即ax≤ex- x2-1
x2-1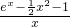
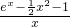 ,则g'(x)=
,则g'(x)=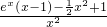
 x2+1则φ′(x)=x(ex-1)
x2+1则φ′(x)=x(ex-1) >0
>0
 即a的取值范围是(-∞,e-
即a的取值范围是(-∞,e- ]
] x2+(a-3)x+1恒成立将a分离出来,然后利用导数研究不等式另一侧函数在[1,+∞)上的最值,即可求出所求.
x2+(a-3)x+1恒成立将a分离出来,然后利用导数研究不等式另一侧函数在[1,+∞)上的最值,即可求出所求.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com