
【题目】下列四个命题:
①函数![]() 的最大值为1;
的最大值为1;
②“若![]() ,则
,则![]() ”的逆命题为真命题;
”的逆命题为真命题;
③若![]() 为锐角三角形,则有
为锐角三角形,则有![]() ;
;
④“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 内单调递增”的充分必要条件.
内单调递增”的充分必要条件.
其中所有正确命题的序号为____________.
【答案】③④
【解析】
利用二倍角公式化简函数,可得![]() ,根据正弦型函数值域可知①错误;确定原命题的逆命题后,通过
,根据正弦型函数值域可知①错误;确定原命题的逆命题后,通过![]() 可知逆命题为假,②错误;利用诱导公式和角的范围可证得结论,③正确;分类讨论去掉函数中的绝对值符号,根据二次函数的性质可确定函数的单调性,从而得到满足题意的范围,进而说明充要条件成立,④正确.
可知逆命题为假,②错误;利用诱导公式和角的范围可证得结论,③正确;分类讨论去掉函数中的绝对值符号,根据二次函数的性质可确定函数的单调性,从而得到满足题意的范围,进而说明充要条件成立,④正确.
①![]()
![]() ,①错误
,①错误
②“若![]() ,则
,则![]() ”的逆命题为:“若
”的逆命题为:“若![]() ,则
,则![]() ”
”
若![]() ,可知
,可知![]() ,则其逆命题为假命题,②错误
,则其逆命题为假命题,②错误
③![]() 为锐角三角形
为锐角三角形 ![]() ,
,![]() ,
,![]()
![]() 且
且![]()
![]()
同理可得:![]() ,
,![]()
![]() ,③正确
,③正确
④令![]() ,解得:
,解得:![]() ,
,![]()
当![]() 时,
时,![]() 对
对![]() 恒成立
恒成立 ![]()
![]() 对称轴为
对称轴为![]()
![]() 在
在![]() 上单调递增,充分条件成立
上单调递增,充分条件成立
当![]() 时,
时,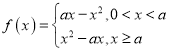 ,此时
,此时![]() 在
在![]() 上单调递减,不满足题意
上单调递减,不满足题意
![]() “
“![]() ”是“
”是“![]() 在区间
在区间![]() 内单调递增”的充分必要条件,④正确
内单调递增”的充分必要条件,④正确
本题正确结果:③④


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】过函数![]() 的图象
的图象![]() 上一点
上一点![]() 作倾斜角互补的两条直线,分别与
作倾斜角互补的两条直线,分别与![]() 交与异于
交与异于![]() 的
的![]() ,
,![]() 两点.
两点.
(1)求证:直线![]() 的斜率为定值;
的斜率为定值;
(2)如果![]() ,
,![]() 两点的横坐标均不大于0,求
两点的横坐标均不大于0,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设F1,F2是椭圆C:![]() (a>b>0)的左、右焦点,直线y=kx(k>0)与椭圆C交于A,B.已知椭圆C的焦距是2,四边形AF1BF2的周长是4
(a>b>0)的左、右焦点,直线y=kx(k>0)与椭圆C交于A,B.已知椭圆C的焦距是2,四边形AF1BF2的周长是4![]() .
.
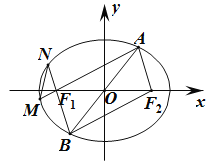
(1)求椭圆C的方程;
(2)直线AF1,BF1分别与椭圆C交于M,N,求△MNF1面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面四边形ABCD中,E、F是AD、BD中点,AB=AD=CD=2, BD=2![]() ,∠BDC=90°,将△ABD沿对角线BD折起至△
,∠BDC=90°,将△ABD沿对角线BD折起至△![]() ,使平面
,使平面![]() ⊥平面BCD,则四面体
⊥平面BCD,则四面体![]() 中,下列结论不正确是 ( )
中,下列结论不正确是 ( )
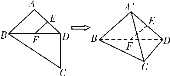
A. EF∥平面![]()
B. 异面直线CD与![]() 所成的角为90°
所成的角为90°
C. 异面直线EF与![]() 所成的角为60°
所成的角为60°
D. 直线![]() 与平面BCD所成的角为30°
与平面BCD所成的角为30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() 平面ABCD,四边形ABCD是矩形,且
平面ABCD,四边形ABCD是矩形,且![]() ,
,![]() ,E是棱BC上的动点,F是线段PE的中点.
,E是棱BC上的动点,F是线段PE的中点.
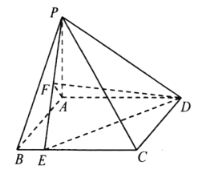
(Ⅰ)求证:![]() 平面ADF;
平面ADF;
(Ⅱ)若直线DE与平面ADF所成角为30°,求EC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊数学家阿波罗尼奧斯(约公元前262~公元前190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,他证明过这样一个命题:平面内与两定点距离的比为常数k(k>0,k≠1)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.在平面直角坐标系中,设A(﹣3,0),B(3,0),动点M满足![]() =2,则动点M的轨迹方程为()
=2,则动点M的轨迹方程为()
A. (x﹣5)2+y2=16B. x2+(y﹣5)2=9
C. (x+5)2+y2=16D. x2+(y+5)2=9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com