
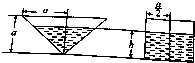
 一个圆锥形容器和一个圆柱形容器的轴截面的尺寸如图,两容器盛有液体的体积正好相等,且液面高均为h,求h.
一个圆锥形容器和一个圆柱形容器的轴截面的尺寸如图,两容器盛有液体的体积正好相等,且液面高均为h,求h.| 1 |
| 3 |
| 1 |
| 3 |
| a |
| 2 |
| a |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| ||
| 2 |


科目:高中数学 来源: 题型:
| 3 |
| sin2θ |
| sinθ-cosθ |
| cos2θ |
| cosθ-sinθ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| e |
查看答案和解析>>
科目:高中数学 来源: 题型:
 将正整数按下表的规律排列,把行与列交叉处的一个数称为某行某列的数,记作aij(i,j∈N*),如第2行第4列的数是15,记作a24=15,则a82是
将正整数按下表的规律排列,把行与列交叉处的一个数称为某行某列的数,记作aij(i,j∈N*),如第2行第4列的数是15,记作a24=15,则a82是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com