Question

在平面直角坐标系中，已知A₁(-3,0)、A₂(3,0),P(x,y),M(,0)，若实数λ使向量、λ、满足λ²·()²=·.

(1)求P点的轨迹方程，并判断P点的轨迹是怎样的曲线；

(2)当λ=时，过点A₁且斜率为1的直线与(1)中的曲线相交的另一点为B，能否在直线x=-9上找一点C，使△A₁BC为正三角形.

Answer 1

解:（1）由已知可得=(x+3,y), =(x-3,y), =(,0),

∵λ²()²=·,

∴λ²(x²-9)=x²-9+y²,

即P点的轨迹方程是(1-λ²)x²+y²=9(1-λ²).

①当1-λ²＞0且λ≠0,即λ∈(-1,0)∪(0,1)时，有=1,P点的轨迹是椭圆.

②当λ=0时，方程x²+y²=9,P的轨迹是圆.

③1-λ²＜0，即λ∈(-∞,-1)∪(1,+∞)时，方程为=1,P点的轨迹是双曲线.

④1-λ²=0，即λ=±1时，方程为y=0, P点的轨迹是直线.

（2）过点A₁且斜率为1的直线方程为y=x＋3.

当λ=时，曲线方程为=1.

由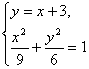得5x²+18x+9=0,x₁=-3,x₂=-.从而|A₁B|=|x₂-x₁|=.

设C（－9，y），|A₁C|=,

因为△A₁BC是正三角形，|A₁B|=|A₁C|，,即y²=-，无解.

所以在直线x=9上找不到点C，使△A₁BC是正三角形.