
【题目】已知函数![]() .
.
(1)设![]() 是
是![]() 的极值点.求
的极值点.求![]() ,并求
,并求![]() 的单调区间;
的单调区间;
(2)证明:当![]() 时,
时,![]() .
.
【答案】(1) a=![]() ;f(x)在(0,2)单调递减,在(2,+∞)单调递增.
;f(x)在(0,2)单调递减,在(2,+∞)单调递增.
(2)证明见解析.
【解析】分析:(1)先确定函数的定义域,对函数求导,利用f ′(2)=0,求得a=![]() ,从而确定出函数的解析式,之后观察导函数的解析式,结合极值点的位置,从而得到函数的增区间和减区间;
,从而确定出函数的解析式,之后观察导函数的解析式,结合极值点的位置,从而得到函数的增区间和减区间;
(2)结合指数函数的值域,可以确定当a≥![]() 时,f(x)≥
时,f(x)≥![]() ,之后构造新函数g(x)=
,之后构造新函数g(x)=![]() ,利用导数研究函数的单调性,从而求得g(x)≥g(1)=0,利用不等式的传递性,证得结果.
,利用导数研究函数的单调性,从而求得g(x)≥g(1)=0,利用不等式的传递性,证得结果.
详解:(1)f(x)的定义域为![]() ,f ′(x)=aex–
,f ′(x)=aex–![]() .
.
由题设知,f ′(2)=0,所以a=![]() .
.
从而f(x)=![]() ,f ′(x)=
,f ′(x)=![]() .
.
当0<x<2时,f ′(x)<0;当x>2时,f ′(x)>0.
所以f(x)在(0,2)单调递减,在(2,+∞)单调递增.
(2)当a≥![]() 时,f(x)≥
时,f(x)≥![]() .
.
设g(x)=![]() ,则
,则![]()
当0<x<1时,g′(x)<0;当x>1时,g′(x)>0.所以x=1是g(x)的最小值点.
故当x>0时,g(x)≥g(1)=0.
因此,当![]() 时,
时,![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,若棱长为
中,若棱长为![]() ,点
,点![]() 分别为线段
分别为线段![]() 、
、![]() 上的动点,则下列结论正确结论的是( )
上的动点,则下列结论正确结论的是( )
A.![]() 面
面![]() B.面
B.面![]() 面
面![]()
C.点F到面![]() 的距离为定值
的距离为定值![]() D.直线
D.直线![]() 与面
与面![]() 所成角的正弦值为定值
所成角的正弦值为定值![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在![]() 上的函数
上的函数![]() 满足如下条件:①函数
满足如下条件:①函数![]() 的图象关于
的图象关于![]() 轴对称;②对于任意
轴对称;②对于任意![]() ,
,![]() ;③当
;③当![]() 时,
时,![]() ;④函数
;④函数![]() ,
,![]() ,若过点
,若过点![]() 的直线
的直线![]() 与函数
与函数![]() 的图象在
的图象在![]() 上恰有8个交点,则直线
上恰有8个交点,则直线![]() 斜率
斜率![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() ,离心率
,离心率![]() ,短轴
,短轴![]() ,抛物线顶点在原点,以坐标轴为对称轴,焦点为
,抛物线顶点在原点,以坐标轴为对称轴,焦点为![]() ,
,
(1)求椭圆和抛物线的方程;
(2)设坐标原点为![]() ,
,![]() 为抛物线上第一象限内的点,
为抛物线上第一象限内的点,![]() 为椭圆是一点,且有
为椭圆是一点,且有![]() ,当线段
,当线段![]() 的中点在
的中点在![]() 轴上时,求直线
轴上时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() ,以原点
,以原点![]() 为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ.
为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ.
(1)若曲线C1方程中的参数是α,且C1与C2有且只有一个公共点,求C1的普通方程;
(2)已知点A(0,1),若曲线C1方程中的参数是t,0<α<π,且C1与C2相交于P,Q两个不同点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如表:
损坏餐椅数 | 未损坏餐椅数 | 总计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总计 | 80 | 320 | 400 |
![]() 求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
![]() 请说明是否有
请说明是否有![]() 以上的把握认为损毁餐椅数量与学习雷锋精神
以上的把握认为损毁餐椅数量与学习雷锋精神
有关?![]() 参考公式:
参考公式:![]() ,
,
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,M是SB的中点,AB∥CD,BC⊥CD,且AB=BC=2,CD=SD=1,又SD⊥面SAB.
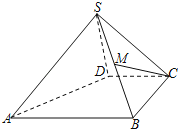
(1)证明:CD⊥SD;
(2)证明:CM∥面SAD;
(3)求四棱锥S﹣ABCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com