
| A. | (-∞,-1] | B. | (-∞,1] | C. | [-1,+∞) | D. | [1,+∞) |
分析 由题意可得可得y′=-sinx+a≥0在[-$\frac{π}{2}$,$\frac{π}{2}$]上恒成立,即 a≥sinx在[-$\frac{π}{2}$,$\frac{π}{2}$]上恒成立,由此求得a的范围.
解答 解:由函数y=cosx+ax在[-$\frac{π}{2}$,$\frac{π}{2}$]上是增函数,可得y′=-sinx+a≥0在[-$\frac{π}{2}$,$\frac{π}{2}$]上恒成立,
即 a≥sinx在[-$\frac{π}{2}$,$\frac{π}{2}$]上恒成立,故a≥1,
故选:D.
点评 本题主要考查利用导数研究函数的单调性,函数的恒成立问题,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | n∥α | B. | n∥α或n?α | C. | n?α或n与α不平行 | D. | n?α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
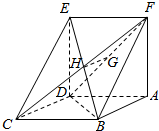 如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点,记CD=x,V(x)表示四棱锥F-ABCD的体积.
如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点,记CD=x,V(x)表示四棱锥F-ABCD的体积.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{7}{8}$ | B. | $\frac{7}{8}$ | C. | $-\frac{1}{8}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) |
| 人数 | 2 | 3 | 15 | 20 | 7 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com