
【题目】已知两点M和N分别在直线y=mx和y=﹣mx(m>0)上运动,且|MN|=2,动点p满足: ![]() (O为坐标原点),点P的轨迹记为曲线C. (I)求曲线C的方程,并讨论曲线C的类型;
(O为坐标原点),点P的轨迹记为曲线C. (I)求曲线C的方程,并讨论曲线C的类型;
(Ⅱ)过点(0,1)作直线l与曲线C交于不同的两点A、B,若对于任意m>1,都有∠AOB为锐角,求直线l的斜率k的取值范围.
【答案】解:(I)由 ![]() ,得P是MN的中点. 设P(x,y),M(x1 , mx1),N(x2 , ﹣mx2)依题意得:
,得P是MN的中点. 设P(x,y),M(x1 , mx1),N(x2 , ﹣mx2)依题意得: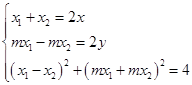
消去x1 , x2 , 整理得  .
.
当m>1时,方程表示焦点在y轴上的椭圆;
当o<m<1时,方程表示焦点在x轴上的椭圆;
当m=1时,方程表示圆.
(II)由m>1,焦点在y轴上的椭圆,直线l与曲线c恒有两交点,
因为直线斜率不存在时不符合题意,
可设直线l的方程为y=kx+1,直线与椭圆的交点为A(x1 , y1),B(x2 , y2).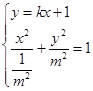 (m4+k2)x2+2kx+1﹣m2=0
(m4+k2)x2+2kx+1﹣m2=0![]() ,
, ![]()
![]()
要使∠AOB为锐角,则有 ![]()
∴x1x2+y1y2= ![]()
即m4﹣(k2+1)m2+1>0,
可得 ![]() ,对于任意m>1恒成立.
,对于任意m>1恒成立.
而 ![]() ,∴K2+1≤2,﹣1≤k≤1
,∴K2+1≤2,﹣1≤k≤1
所以满足条件的k的取值范围是[﹣1.1]
【解析】(I)根据题意可判断出P是MN的中点.设出P,M,N的坐标,根据题意联立方程求得 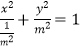 ,然后对m>1,o<m<1和m=1对方程表示出曲线进行分类讨论.(II)设出直线l的方程,与椭圆的方程联立消去y,利用韦达定理表示出x1+x2和x1x2 , 利用直线方程表示出y1y2 , 要使∠AOB为锐角,需
,然后对m>1,o<m<1和m=1对方程表示出曲线进行分类讨论.(II)设出直线l的方程,与椭圆的方程联立消去y,利用韦达定理表示出x1+x2和x1x2 , 利用直线方程表示出y1y2 , 要使∠AOB为锐角,需 ![]() ,利用向量的基本运算整理得
,利用向量的基本运算整理得 ![]() ,利用基本不等式求得
,利用基本不等式求得 ![]() 进而求得k的范围.
进而求得k的范围.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
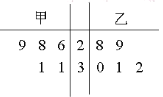
①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的标号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张三同学从每年生日时对自己的身高测量后记录如表:
![]()
(附:回归直线的斜率和截距的最小二乘法估计公式分别为: ,
,![]() )
)
(1)求身高![]() 关于年龄
关于年龄![]() 的线性回归方程;(可能会用到的数据:
的线性回归方程;(可能会用到的数据:![]() (cm))
(cm))
(2)利用(1)中的线性回归方程,分析张三同学![]() 岁起到
岁起到![]() 岁身高的变化情况,如
岁身高的变化情况,如 ![]() 岁之前都符合这一变化,请预测张三同学
岁之前都符合这一变化,请预测张三同学 ![]() 岁时的身高。
岁时的身高。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一支车队有![]() 辆车,某天依次出发执行运输任务。第一辆车于下午
辆车,某天依次出发执行运输任务。第一辆车于下午![]() 时出发,第二辆车于下午
时出发,第二辆车于下午![]() 时
时![]() 分出发,第三辆车于下午
分出发,第三辆车于下午![]() 时
时![]() 分出发,以此类推。假设所有的司机都连续开车,并都在下午
分出发,以此类推。假设所有的司机都连续开车,并都在下午![]() 时停下来休息.
时停下来休息.
到下午![]() 时,最后一辆车行驶了多长时间?
时,最后一辆车行驶了多长时间?
如果每辆车的行驶速度都是![]() ,这个车队当天一共行驶了多少
,这个车队当天一共行驶了多少![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一支车队有![]() 辆车,某天依次出发执行运输任务。第一辆车于下午
辆车,某天依次出发执行运输任务。第一辆车于下午![]() 时出发,第二辆车于下午
时出发,第二辆车于下午![]() 时
时![]() 分出发,第三辆车于下午
分出发,第三辆车于下午![]() 时
时![]() 分出发,以此类推。假设所有的司机都连续开车,并都在下午
分出发,以此类推。假设所有的司机都连续开车,并都在下午![]() 时停下来休息.
时停下来休息.
到下午![]() 时,最后一辆车行驶了多长时间?
时,最后一辆车行驶了多长时间?
如果每辆车的行驶速度都是![]() ,这个车队当天一共行驶了多少
,这个车队当天一共行驶了多少![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱A1B1C1﹣ABC中, ![]() ,AB=AC=AA1=1,已知G和E分别为A1B1和CC1的中点,D与F分别为线段AC和AB上的动点(不包括端点),若GD⊥EF,则线段DF的长度的取值范围为( )
,AB=AC=AA1=1,已知G和E分别为A1B1和CC1的中点,D与F分别为线段AC和AB上的动点(不包括端点),若GD⊥EF,则线段DF的长度的取值范围为( )
A.[ ![]() ,1)
,1)
B.[ ![]() ,1]
,1]
C.( ![]() ,1)
,1)
D.[ ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现给出以下四个命题:
①已知![]() 中,角A,B,C的对边为a,b,c,当
中,角A,B,C的对边为a,b,c,当![]() ,
,![]() ,
,![]() 时,满足条件的三角形共有1个;
时,满足条件的三角形共有1个;
②已知![]() 中,角A,B,C的对边为a,b,c,若三角形
中,角A,B,C的对边为a,b,c,若三角形![]() ,这个三角形的最大角是
,这个三角形的最大角是![]() ;
;
③设![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() 是两个不同的平面,若
是两个不同的平面,若![]() ,
,![]() ,则
,则![]() ;
;
④设![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() 是两个不同的平面,若
是两个不同的平面,若![]() ,
,![]() ,则
,则![]()
其中正确的序号是__________(写出所有正确说法的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com