
【题目】函数f(x)=log ![]() (x2﹣ax+3)在(﹣∞,1)上单调递增,则a的范围是( )
(x2﹣ax+3)在(﹣∞,1)上单调递增,则a的范围是( )
A.(2,+∞)
B.[2,+∞)
C.[2,4]
D.[2,4)
科目:高中数学 来源: 题型:
【题目】某校高二年级进行了百科知识大赛,为了了解高二年级900名同学的比赛情况,现在甲、乙两个班级各随机抽取了10名同学的成绩,比赛成绩满分为100分,80分以上可获得二等奖,90分以上可以获得一等奖,已知抽取的两个班学生的成绩(单位:分)数据的茎叶图如图1所示:

(1)比较两组数据的分散程度(只需要给出结论),并求出甲组数据的频率分布直方图如图2中所示的![]() 值;
值;
(2)现从两组数据中获奖的学生里分别随机抽取一人接受采访,求被抽中的甲班学生成绩高于乙班学生成绩的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)若直线![]() 过焦点
过焦点![]() ,且与圆
,且与圆![]() 交于
交于![]() (其中
(其中![]() 在
在![]() 轴同侧),求证:
轴同侧),求证: ![]() 是定值;
是定值;
(Ⅱ)设抛物线![]() 在
在![]() 和
和![]() 点的切线交于点
点的切线交于点![]() ,试问:
,试问: ![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为菱形?若存在,请说明理由并求此时直线
为菱形?若存在,请说明理由并求此时直线![]() 的斜率和点
的斜率和点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的定义域是[0,2],则函数g(x)= ![]() 的定义域是( )
的定义域是( )
A.[0,1)∪(1,2]
B.[0,1)∪(1,4]
C.[0,1)
D.(1,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱锥P -ABC中,PA⊥底面ABC,∠BCA![]() 90°,AP
90°,AP![]() AC,点D,E分别在棱PB,PC上,且BC∥平面ADE.
AC,点D,E分别在棱PB,PC上,且BC∥平面ADE.

(Ⅰ)求证:DE⊥平面PAC;
(Ⅱ)若PC⊥AD,且三棱锥P-ABC的体积为8,求多面体ABCED的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm),根据所得数据画出的样本频率分布直方图如图,那么在这片树木中底部周长大于100cm的株树大约中( ) 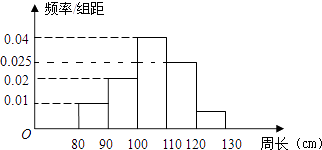
A.3000
B.6000
C.7000
D.8000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com