
【题目】如图,四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 上一点,
上一点, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.

(1)证明: ![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)见解析;(2) 所求角的余弦值![]() .
.
【解析】试题分析:(1)设![]() 的中点
的中点![]() ,连接
,连接![]() ,,由三角形中位线定理结合已知可得四边形
,,由三角形中位线定理结合已知可得四边形![]() 为平行四边形,得到
为平行四边形,得到![]() .再由线面平行的判定可得MN∥平面PAB;
.再由线面平行的判定可得MN∥平面PAB;
(2)取![]() 边的靠近点
边的靠近点![]() 的四等分点
的四等分点![]() ,连接
,连接![]() ,
, ![]() ,可证异面直线
,可证异面直线![]() 与
与![]() 所成角就等于
所成角就等于![]() 与
与![]() 所成的角,则在
所成的角,则在![]() 中设法求出
中设法求出![]() ,
, ![]() 和
和![]() 最后由余弦定理可求求异面直线
最后由余弦定理可求求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
试题解析(1)由已知得![]() ,
,
取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
由![]() 为
为![]() 中点知
中点知![]() ,
, ![]() .
.
又![]() ,故
,故![]() 平行且等于
平行且等于![]() ,
,
四边形![]() 为平行四边形,于是
为平行四边形,于是![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)取![]() 边的靠近点
边的靠近点![]() 的四等分点
的四等分点![]() ,连接
,连接![]() ,
, ![]() ,则
,则![]() ,
,
由![]()
![]() 四边形
四边形![]() 为平行四边形
为平行四边形
所以异面直线![]() 与
与![]() 所成角就等于
所成角就等于![]() 与
与![]() 所成的角
所成的角
![]() ,
, ![]() ,
, ![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
, ![]() ,
, ![]()
![]()
![]()
![]()
所以所求角的余弦值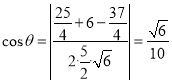


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机购为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事用户车盈利10000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有六辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选两辆车,求这两辆车恰好有一辆为事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,上、下顶点分别为
,上、下顶点分别为![]() 、
、![]() ,
, ![]() 为坐标原点,四边形
为坐标原点,四边形![]() 的面积为
的面积为![]() ,且该四边形内切圆的方程为
,且该四边形内切圆的方程为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 、
、![]() 是椭圆
是椭圆![]() 上的两个不同的动点,直线
上的两个不同的动点,直线![]() 、
、![]() 的斜率之积等于
的斜率之积等于![]() ,试探求
,试探求![]() 的面积是否为定值,并说明理由.
的面积是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】团购已成为时下商家和顾客均非常青睐的一种省钱、高校的消费方式,不少商家同时加入多家团购网.现恰有三个团购网站在![]() 市开展了团购业务,
市开展了团购业务, ![]() 市某调查公司为调查这三家团购网站在本市的开展情况,从本市已加入了团购网站的商家中随机地抽取了50家进行调查,他们加入这三家团购网站的情况如下图所示.
市某调查公司为调查这三家团购网站在本市的开展情况,从本市已加入了团购网站的商家中随机地抽取了50家进行调查,他们加入这三家团购网站的情况如下图所示.
(1)从所调查的50家商家中任选两家,求他们加入团购网站的数量不相等的概率;
(2)从所调查的50家商家中任取两家,用![]() 表示这两家商家参加的团购网站数量之差的绝对值,求随机变量
表示这两家商家参加的团购网站数量之差的绝对值,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(3)将频率视为概率,现从![]() 市随机抽取3家已加入团购网站的商家,记其中恰好加入了两个团购网站的商家数为
市随机抽取3家已加入团购网站的商家,记其中恰好加入了两个团购网站的商家数为![]() ,试求事件“
,试求事件“![]() ”的概率.
”的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=3n+m(m为常数,n∈N+)
(1)求a1 , a2 , a3;
(2)若数列{an}为等比数列,求常数m的值及an;
(3)对于(2)中的an , 记f(n)=λa2n+1﹣4λan+1﹣7,若f(n)<0对任意的正整数n恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次爱心捐款活动中,小李为了了解捐款数额是否和居民自身的经济收入有关,随机调査了某地区的![]() 个捐款居民每月平均的经济收入. 在捐款超过
个捐款居民每月平均的经济收入. 在捐款超过![]() 元的居民中,每月平均的经济收入没有达到
元的居民中,每月平均的经济收入没有达到![]() 元的有
元的有![]() 个,达到
个,达到![]() 元的有
元的有![]() 个;在捐款不超过
个;在捐款不超过![]() 元的居民中,每月平均的经济收入没有达到
元的居民中,每月平均的经济收入没有达到![]() 元的有
元的有![]() 个.
个.
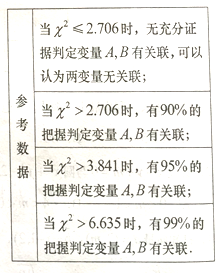
(1)在下图表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额是否超过
以上的把握认为捐款数额是否超过![]() 元和居民毎月平均的经济收入是否达到
元和居民毎月平均的经济收入是否达到![]() 元有关?
元有关?
(2)将上述调查所得到的频率视为概率. 现在从该地区大量居民中,采用随机抽样方法毎次抽取![]() 个居民,共抽取
个居民,共抽取![]() 次,记被抽取的
次,记被抽取的![]() 个居民中经济收入达到
个居民中经济收入达到![]() 元的人数为
元的人数为![]() ,求
,求![]() 和期望
和期望![]() 的值.
的值.
每月平均经济收入达到 | 每月平均经济收入没有达到 | 合计 | |
捐款超过 | |||
捐款不超过 | |||
合计 |
附: 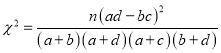 ,其中
,其中![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com