
【题目】某学校为了解高三复习效果,从高三第一学期期中考试成绩中随机抽取50名考生的数学成绩,分成6组制成频率分布直方图如图所示:
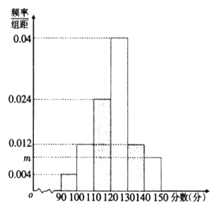
(1)求![]() 的值;并且计算这50名同学数学成绩的样本平均数
的值;并且计算这50名同学数学成绩的样本平均数![]() ;
;
(2)该学校为制定下阶段的复习计划,从成绩在![]() 的同学中选出3位作为代表进行座谈,记成绩在
的同学中选出3位作为代表进行座谈,记成绩在![]() 的同学人数位
的同学人数位![]() ,写出
,写出![]() 的分布列,并求出期望.
的分布列,并求出期望.
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)设![]() 为
为![]() 上的一点,满足
上的一点,满足![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知鸡的产蛋量与鸡舍的温度有关,为了确定下一个时段鸡舍的控制温度,某企业需要了解鸡舍的温度![]() (单位:℃),对某种鸡的时段产蛋量
(单位:℃),对某种鸡的时段产蛋量![]() (单位:
(单位: ![]() )和时段投入成本
)和时段投入成本![]() (单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度
(单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度![]() 和产蛋量
和产蛋量![]() 的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.

|
|
|
|
|
|
|
17.40 | 82.30 | 3.6 | 140 | 9.7 | 2935.1 | 35.0 |
其中![]() .
.
(1)根据散点图判断, ![]() 与
与![]() 哪一个更适宜作为该种鸡的时段产蛋量
哪一个更适宜作为该种鸡的时段产蛋量![]() 关于鸡舍时段控制温度
关于鸡舍时段控制温度![]() 的回归方程类型?(给判断即可,不必说明理由)
的回归方程类型?(给判断即可,不必说明理由)
(2)若用![]() 作为回归方程模型,根据表中数据,建立
作为回归方程模型,根据表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知时段投入成本![]() 与
与![]() 的关系为
的关系为![]() ,当时段控制温度为28℃时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
,当时段控制温度为28℃时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
附:①对于一组具有有线性相关关系的数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为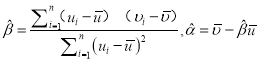
②
|
|
|
|
|
0.08 | 0.47 | 2.72 | 20.09 | 1096.63 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥曲线 (
(![]() 是参数)和定点
是参数)和定点![]() ,
,![]() 、
、![]() 是圆锥曲线的左、右焦点.
是圆锥曲线的左、右焦点.
(1)求经过点![]() 且垂直于直线
且垂直于直线![]() 的直线
的直线![]() 的参数方程;
的参数方程;
(2)以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,求直线
轴的正半轴为极轴建立极坐标系,求直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并求出函数![]() 的解析式;
的解析式;
(2)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com