
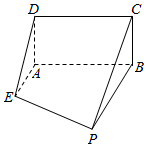
 如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面,平面ABCD∩平面ABPE=AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.
如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面,平面ABCD∩平面ABPE=AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.分析 (I)证明BP⊥平面ABCD,以B为原点建立坐标系,则$\overrightarrow{BP}$为平面ABCD的法向量,求出$\overrightarrow{EM}•\overrightarrow{BP}$=-1×0+0×2+$\frac{1}{2}×0$=0,从而有EM∥平面ABCD;
(II)假设存在点N符合条件,设$\overrightarrow{PN}$=λ$\overrightarrow{PD}$,求出$\overrightarrow{BN}$,平面PCD的法向量$\overrightarrow{n}$的坐标,令|cos<$\overrightarrow{BN}$,$\overrightarrow{n}$>|=$\frac{2}{\sqrt{5}•\sqrt{9{λ}^{2}-8λ+4}}$=$\frac{2}{5}$解出λ,根据λ的值得出结论.
解答  (Ⅰ)证明:∵平面ABCD⊥平面ABEP,平面ABCD∩平面ABEP=AB,BP⊥AB
(Ⅰ)证明:∵平面ABCD⊥平面ABEP,平面ABCD∩平面ABEP=AB,BP⊥AB
∴BP⊥平面ABCD,又AB⊥BC,
∴直线BA,BP,BC两两垂直,
以B为原点,分别以BA,BP,BC为x轴,y轴,z轴建立如图所示的空间直角坐标系.
则P(0,2,0),B(0,0,0),D(2,0,1),E(2,1,0),C(0,0,1),∴M(1,1,$\frac{1}{2}$),
∴$\overrightarrow{EM}$=(-1,0,$\frac{1}{2}$),$\overrightarrow{BP}$=(0,2,0).
∵BP⊥平面ABCD,∴$\overrightarrow{BP}$为平面ABCD的一个法向量,
∵$\overrightarrow{EM}•\overrightarrow{BP}$=-1×0+0×2+$\frac{1}{2}×0$=0,
∴$\overrightarrow{EM}$⊥$\overrightarrow{BP}$.又EM?平面ABCD,
∴EM∥平面ABCD.
(Ⅱ)解:当点N与点D重合时,直线BN与平面PCD所成角的正弦值为$\frac{2}{5}$.
理由如下:
∵$\overrightarrow{PD}$=(2,-2,1),$\overrightarrow{CD}$=(2,0,0),
设平面PCD的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{2x=0}\\{2x-2y+z=0}\end{array}\right.$.
令y=1,得$\overrightarrow{n}$=(0,1,2).
假设线段PD上存在一点N,使得直线BN与平面PCD所成角α的正弦值等于$\frac{2}{5}$.
设$\overrightarrow{PN}$=λ$\overrightarrow{PD}$=(2λ,-2λ,λ)(0≤λ≤1),∴$\overrightarrow{BN}$=$\overrightarrow{BP}$+$\overrightarrow{PN}$=(2λ,2-2λ,λ).
∴|cos<$\overrightarrow{BN}$,$\overrightarrow{n}$>|=$\frac{2}{\sqrt{5}•\sqrt{9{λ}^{2}-8λ+4}}$=$\frac{2}{5}$.
∴9λ2-8λ-1=0,解得λ=1或$\frac{1}{9}$(舍去).
∴当N点与D点重合时,直线BN与平面PCD所成角的正弦值等于$\frac{2}{5}$.
点评 本题考查了线面平行的判断,空间向量的应用与线面角的计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 充分必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
| 对服务好评 | 对服务不满意 | 合计 | |
| 对商品好评 | a=80 | b=40 | 120 |
| 对商品不满意 | c=70 | d=10 | 80 |
| 合计 | 150 | 50 | n=200 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点C是圆O直径BE的延长线上一点,AC是圆O的切线,A为切点,∠ACB的平分线CD分别与AB、AE交于D、F.
如图,点C是圆O直径BE的延长线上一点,AC是圆O的切线,A为切点,∠ACB的平分线CD分别与AB、AE交于D、F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{9}$ | B. | $\frac{19}{10}$ | C. | $\frac{9}{5}$ | D. | $\frac{11}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 29 | B. | 47 | C. | 76 | D. | 123 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com